Softmax回归（Softmax Regression）

转载请注明出处：http://www.cnblogs.com/BYRans/

多分类问题

在一个多分类问题中，因变量y有k个取值，即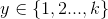。例如在邮件分类问题中，我们要把邮件分为垃圾邮件、个人邮件、工作邮件3类，目标值y是一个有3个取值的离散值。这是一个多分类问题，二分类模型在这里不太适用。

多分类问题符合多项分布。有许多算法可用于解决多分类问题，像决策树、朴素贝叶斯等。这篇文章主要讲解多分类算法中的Softmax回归（Softmax Regression)

推导思路为：首先证明多项分布属于指数分布族，这样就可以使用广义线性模型来拟合这个多项分布，由广义线性模型推导出的目标函数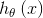即为Softmax回归的分类模型。

证明多项分布属于指数分布族

多分类模型的输出结果为该样本属于k个类别的概率，从这k个概率中我们选择最优的概率对应的类别（通常选概率最大的类别），作为该样本的预测类别。这k个概率用k个变量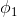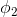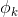，…，表示。这个k变量和为1，即满足：

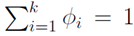
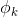可以用前k-1个变量来表示，即：

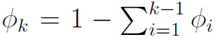
使用广义线性模型拟合这个多分类问题，首先要验证这个多项分布是否符合一个指数分布族。定义T(y)为：

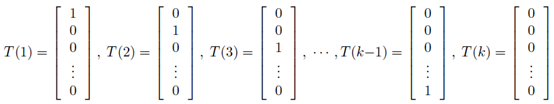
在这里，统计分量T(y)并没有像之前那样定义为T(y)=y，因为T(y)不是一个数值，而是一个k-1维的向量。使用符号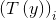表示向量T(y)的第i个元素。

在这里引入一个新符号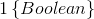：，如果括号内为true则这个符号取1，反之取0，即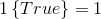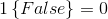，。所以，T(y)与y的关系就可以表示为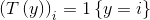

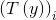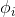与关系为：

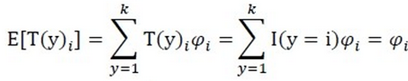
即：

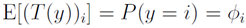
多项分布表达式转化为指数分布族表达式过程如下：

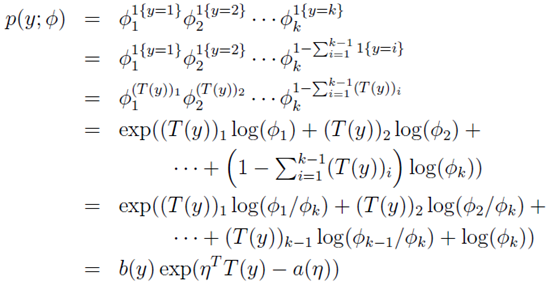
其中：

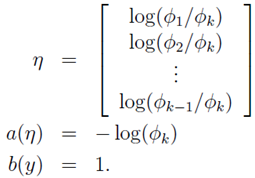
变换过程：

第一步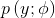：取值为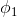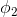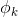，…，中的一个，取决于y的取值。当y=i时，这一步可以理解为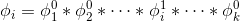

第二步：消去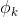

第三步：根据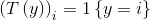

第四、五步：转换为广义线性模型的表达格式。

多项分布表达式可以表示为指数分布族表达式的格式，所以它属于指数分布族，那么就可以用广义线性模型来拟合这个多项式分布模型。

Softmax函数（Softmax Function）

在使用广义线性模型拟合这个多项式分布模型之前，需要先推导一个函数，这个函数在广义线性模型的目标函数中会用到。这个函数称为Softmax函数（Softmax Function）。

由η表达式可得：

这是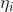关于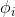的表达式，把它转化为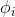关于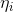的表达式过程为：

为了方便，令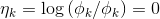，那么

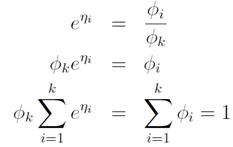
因为：

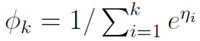
所以：

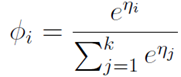
这个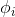关于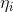的的函数称为Softmax函数（Softmax Function）。

使用广义线性构建模型

根据广义线性模型的假设3:

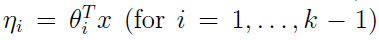
θ是模型中的参数，为了符号上的方便我们定义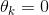，所以

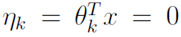
所以模型在给定x的条件下y的分布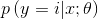为：

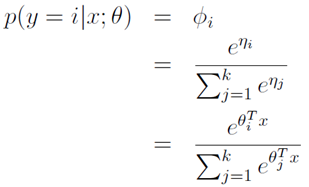
上面的表达式求解的是在y=i时的概率。在Softmax回归这个广义线性模型中，目标函数是：

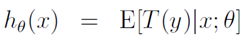
Softmax回归目标函数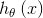的输出是k个概率，即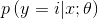其中i=1,2,…,k(虽然输出的是k-1个值，但是第k个值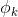可以由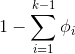求出），求解了这个目标函数，我们就构造出了分类模型。

目标函数推导过程如下：

现在求解目标函数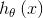还差最后一步：参数拟合的问题。跟我们之前的参数拟合方法类似，我们有m个训练样本，θ的似然函数为：

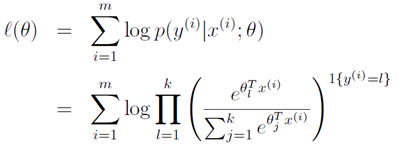
最大化似然函数来求解最优的参数θ，可以使用梯度上升或者牛顿方法。

求解了最优的参数θ后，就可以使用目标函数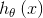进行分类。使用函数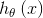进行多分类的方式就叫Softmax回归（Softmax Regression)

Softmax回归 VS k个二元分类器

　　如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用softmax分类器呢，还是使用logistic回归算法建立 k个独立的二元分类器呢？

　　这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）

　　如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的logistic回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。