JDK API从下载到使用

经常有人问我一些java常用类的使用方法，还有一些问某个常用类是干啥的。这些问题都是不会查询jdk api，对常用类的方法不熟悉等情况。于是，经过再三思考决定编写jdk api查询使用手册。

　　☆准备工作

　　①，浏览器能上网②，英语翻译软件(下载中文的可不用)③，已安装jdk

　　☆下载api帮助

　　多年前，曾有热心肠的人，将英文版的api帮助文档翻译成中文版，此版为jdk1.6中文版。所以，我们可以在网络去下载中文版的，还可以下载最新版的英文版的对照查看。目前市面上没有1.6以后的中文版，所以到目前为止比较高的就是1.6的中文版。

　　在百度搜索网站输入 jdk1.6中文版。选择chm格式的下载，chm为帮助文档，查询快捷，使用方便。该文件大小约为34M到37M之间(请确认大小)。

　　

　　右键另存为 你要保存的位置，一般我选择存在页面。

　　

　　然后，去桌面查看，这个文件就是。打开这个文件，将chm格式的文件拖出来。

　　

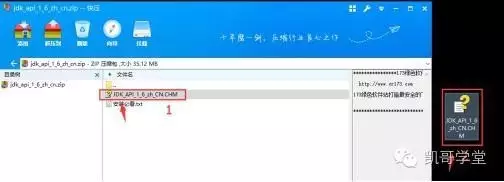
　　选择压缩包1位置处的文件，按住左边不松，然后拉到桌面松开，就解压出来2这样形状的帮助文件。

　　☆ 介绍JDK API帮助文档

　　

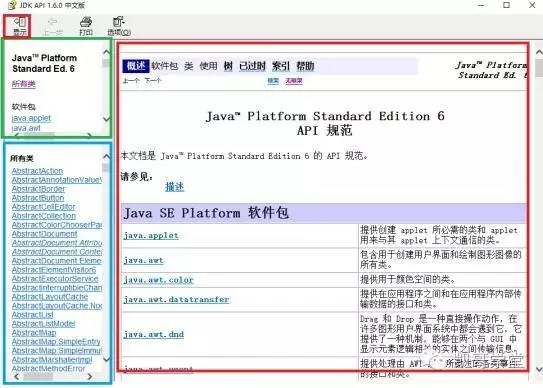
　　打开JDK API文档,我们看到的左边上半部分为所有包的介绍，左边下半部分为包内文件的介绍，而右边则是对左边选中的类的介绍。

　　☆ 使用JDK API查询

　　我们在这里选择Scanner这个类为例。首先，我在打开的api 上面的菜单项找”显示”，然后点击它。然后当前api变为三栏，这可以忽略，点击“索引(N)”这项。

　　

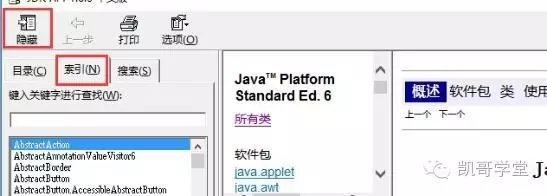
　　接下来，在”输入关键字进行查询(W)”下面的文本框输入Scanner，然后看到下面出现这个选中Scanner，双击它或按回车。

　　

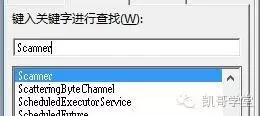
　　弹出这个框

　　

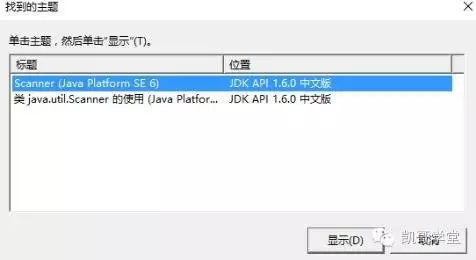
　　这个是询问你是否打开Scanner的说明页面，点击显示按钮即可。

　　

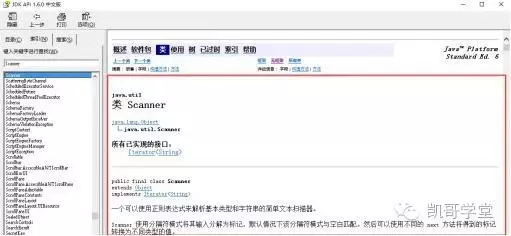
　　此时，我们看到的右边这一部分就是对常用类Scanner的说明。你也是输入System,Math等。

　　☆ api的查询说明

　　大部分人都能查询到如图所示的界面，可以不知道该怎么找。

　　那么，我们首先来看最上面

　　

　　java.util 是说Scanner是在这个包下，使用Scanner是，需要引入java.util.Scanner这个包，接着很清楚说明Scanner是一个类，在下面结构说的是Scanner的继承结构。最下面是关于Scanner实现的接口。(这里我知道引入那个包名即可)

　　

　　下面汉字，说明这个是干什么用的。

　　

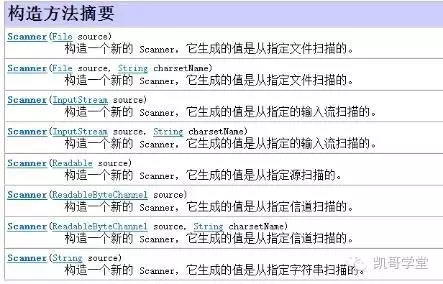
　　构造方法摘要，说明Scanner有那些构造方法，参数分别都可以传入什么类型和格式。

　　

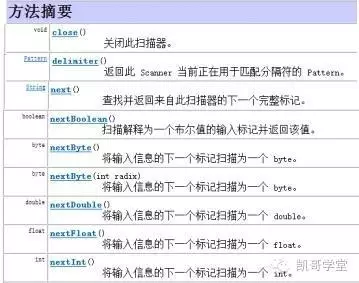
　　方法摘要，说明Scanner提供的方法都有那些，分别描述方法干什么的。

　　比如，看nextInt()这个方法，点击它，就会看到如下图所示

　　

　　这是，看到nextInt() 前是int类型，说明返回时一个int类型，下面返回处已说的相当明确。于是，就有了

　　Scanner sc = new Scanner(System.in);//实例化扫描器int a = sc.nextlnt();// 扫描一个int的存给变量a

　　其他的方法按照类型的方法查询。

　　☆ 说明

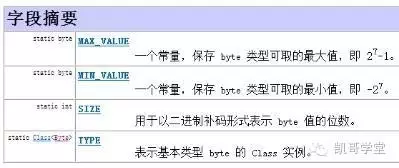
　　①，对于有的类说还有 字段摘要这项，这是对当前类的属性和常量说明。

　　

　　②，有的api使用后，桌面会生成一个.chw格式的缓存文件，关闭api后，删掉这个文件即可。

　　

　　③，对于一些方法可以在搜索选项中找，这里就不解说。

　　曾有大神曰：学习JavaSE，玩的就是API。

技术分享：www.kaige123.com