Codeforces Round #710 (Div. 3) Editorial 1506A - Strange Table

题目链接 https://codeforces.com/contest/1506/problem/A

原题

1506A - Strange Table

Example

input

5
1 1 1
2 2 3
3 5 11
100 100 7312
1000000 1000000 1000000000000

output

1
2
9
1174
1000000000000

题解

先竖列竖列地排数字, 找到x所在的位置s1;

再横行横行地排, 找到s1位置的值并输出

 -----> 

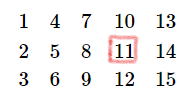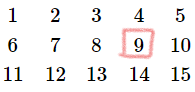
(n为总行数, m为总列数, x为要找的数)

结果 = (行数-1)*m+第几列

求行: 要找到这个数的上一行, 这样用取余(x-1) % n, 比如

10, 我们要得到的是(行数-1) = 0

11, 我们要得到的是(行数-1) = 1

12, 我们要得到的是(行数-1) = 2

 求列: 用除法(x-1) / n+1, 看下上面的图应该就会了

代码

#include <iostream>

using namespace std;
typedef long long ll;
int main()
{
    int t;
    cin >> t;
    while(t --)
    {
        ll n ,m,x;
        scanf("%lld%lld%lld", &n, &m, &x);

        ll l = (x-1) / n+1;
        ll r = (x-1) % n;

        cout << r*m+l << endl;
    }
    return 0;
}