char的越界赋值即其原理剖析

思考：

int ch = ‘A’;

int ch1 = 65;

int ch2 = 321;

printf("%c %c %c\n", ch, ch1, ch2);的输出结果是什么？

char ch = 0;

char ch1 = -128;

char ch2 = 128;

char ch3 = 256;

printf("%d %d %d %d\n", ch, ch1, ch2, ch3);的输出结果又是什么？

我们都知道，char字符类型根据ASCII码表中的ascii值显示字符，并且char类型的范围为-128~127，但是像char ch = 256;这种赋值仍然可以赋值成功，通过上面的思考我已经有了一定的猜想。



输出结果：A A A 0 -128 -128 0

---

猜想：

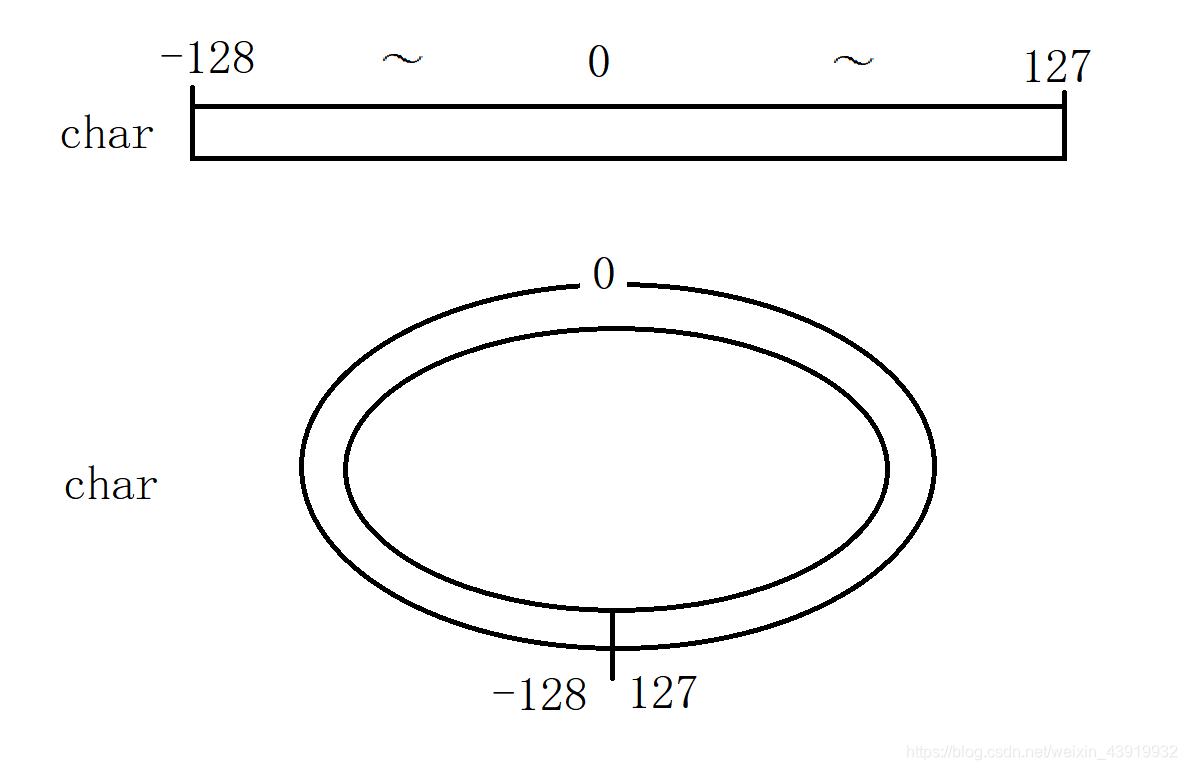
char类型的范围为-128~127

1. char ch1 = 128;输出：-128
   
   　分析：127为char的右极限值，-128位char的左极限值
2. char ch3 = 256;输出：0
   
   　分析：256为char的容量

总结：当输入的值大于char的一边极限值时，会从另一边开始以剩余的差值计算。





测试：

#include <stdio.h>

int main()
{
	char ch;
	for (int i = 0; i <= 512; i++)
	{
		ch = i;
		printf("%d   ->    %d\n", i, ch);
	}

	return 0;
}

输出：

0   ->    0
1   ->    1
2   ->    2
省略部分输出结果 ……
127   ->    127		//char -128~127
128   ->    -128
129   ->    -127
省略部分输出结果 ……
254   ->    -2
255   ->    -1
256   ->    0
257   ->    1
258   ->    2
省略部分输出结果 ……
510   ->    -2
511   ->    -1
512   ->    0

很好，测试结果与我们猜想的一致，那么问题又来了，究竟是不是所有的类型赋值方法都是这样呢，还是只有char是个特例呢？

unsigned char测试

	//unsigned char 0 ~ 255
	unsigned char ch = 0;		//0
	unsigned char ch1 = -1;		//255  = 256 -1
	unsigned char ch2 = 256;	//0    = 0+256
	unsigned char ch3 = 250;	//250  = 0+255
	unsigned char ch4 = 300;	//44   = 256+44
	unsigned char ch5 = 400;	//144  = 256+144
	unsigned char ch6 = -200;	//56   = 256 - 200

unsigned char类型容量为256，则256的倍数全为0（循环一圈回到0位置），可以根据这一特点计算。

例如：

• 正数n(>255)
  • 256的倍数 　　　　0
  • n == k×256＋ｘ　　x
• 负数n(>255)
  • 256的倍数 　　　　0
  • n == －k×256＋ｘ　x

对于char类型，也可以根据取值范围整理出相应的计算公式。大家可对照测试结果自行整理。

---

此外，int unsigned in short ……等中应该也成立，这里就不再做测试。

另附上

　 int 越界处理：可以通过位运算的方式求得各类型的取值范围。

　 '\ddd’转义字符与八进制转换：char类型的其他赋值方式