BUUCTF-LSB
LSB
看到这个题目应该是LSB隐写,StegSolve打开,在红绿蓝0号上发现图片信息
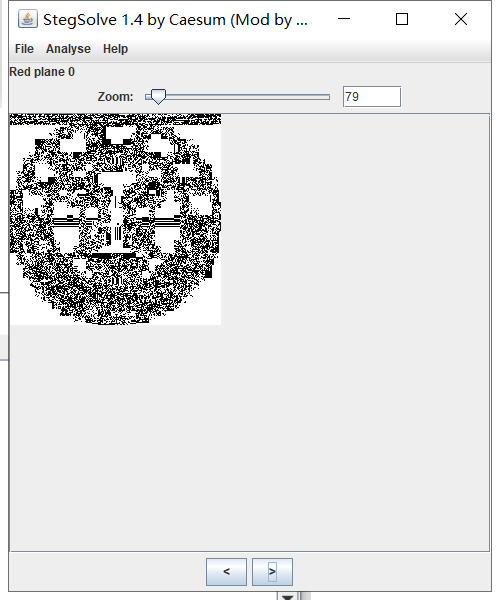
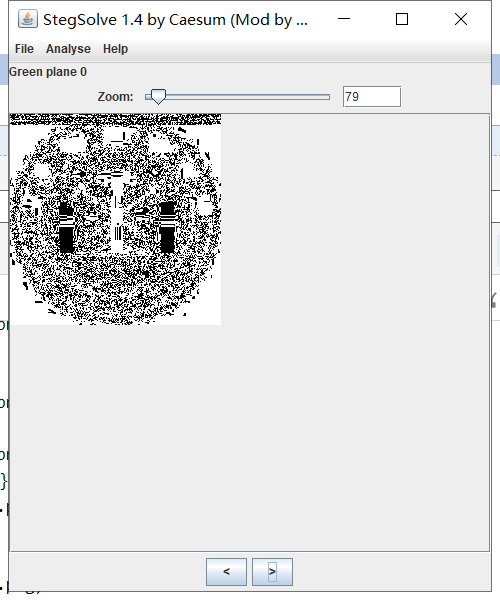
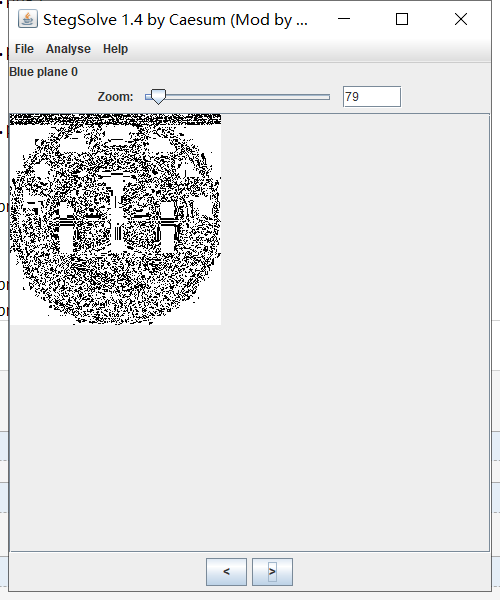
然后在Analyse选择data extract Save bin保存图片即可
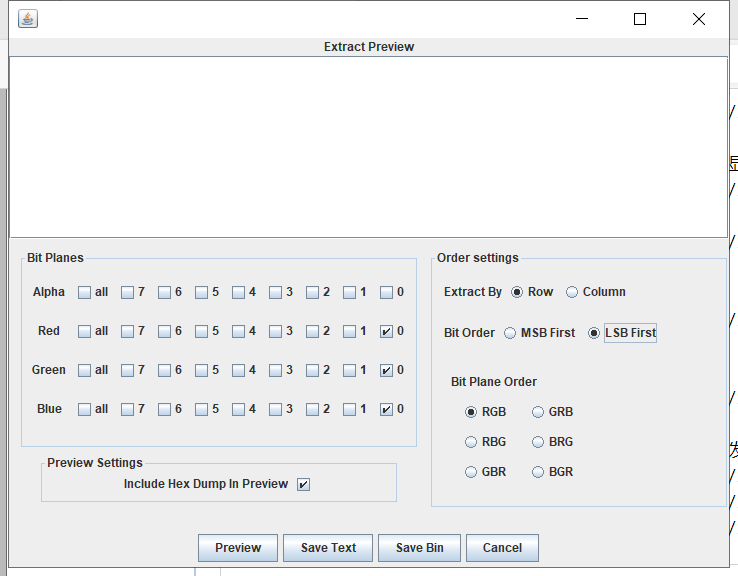
得到的是个二维码,解码即可。
BUUCTF-LSB的更多相关文章
- buuctf misc 刷题记录
1.金三胖 将gif分离出来. 2.N种方法解决 一个exe文件,果然打不开,在kali里分析一下:file KEY.exe,ascii text,先txt再说,base64 图片. 3.大白 crc ...
- buuctf misc wp 02
buuctf misc wp 02 7.LSB 8.乌镇峰会种图 9.rar 10.qr 11.ningen 12.文件中的秘密 13.wireshark 14.镜子里面的世界 15.小明的保险箱 1 ...
- Linux Standards Base LSB
LSB简介 http://www.ibm.com/developerworks/cn/linux/l-lsb-intr/ http://refspecs.linuxbase.org/ http://t ...
- 字节序相关问题简单总结,LSB与MSB
细细碎碎的知识点还真是不少啊,今天总结下通信中的数据字节序的问题. 先来认识名词: MSB:Most Significant Bit. “最高有效位” LSB:Least Significant ...
- LSB最低有效位隐写入门
LSB也就是最低有效位 (Least Significant Bit) 被替换成传递的信息字节.对原图影响很小. 这题可以算是隐写工具[wbStego]的使用入门练习题吧. 第一步,告诉你工具是支持在 ...
- LSB 简介
前 Linux 的发行版非常繁多,为了促进 Linux 不同发行版间的兼容性,LSB(Linux Standards Base)开发了一系列标准,使各种软件可以很好地在兼容 LSB 标准的系统上运行, ...
- Linux就这个范儿 第19章 团结就是力量 LSB是Linux标准化基地(Linux Standards Base)的简称
Linux就这个范儿 第19章 团结就是力量 LSB是Linux标准化基地(Linux Standards Base)的简称 这个图片好可爱,它是LSB组织的图标.你肯定会问:“图标这么设计一定有说 ...
- LSB和MSB
最低有效位(the least significant bit,lsb)是指一个二进制数字中的第0位(即最低位),具有权值为2^0,可以用它来检测数的奇偶性.与之相反的称之为最高有效位.在大端序中,l ...
- 【centos7】 Failed to start LSB Bring up/down
今天碰到几个问题: 1. Failed to start LSB Bring up/down 归结一下 百度 的答案: 1). 90% 修改MAC 地址 2).10% 重启 networkmanage ...
- CentOS7 Failed to start LSB: Bring up/down解决方法
刚刚装好的虚拟机突然不能上网了,报错很诡异,具体报错如下: /etc/init.d/network restart Restarting network (via systemctl): Job f ...
随机推荐
- Kubernetes架构-图解
- 1、【Python运维脚本】Python 按时间删除和清空文件
删除和清空文件,用shell的话一条命令就够了,Python要一堆命令. 但是为了学习Python,所以用于实战,就得这么干了. Python 按时间删除和清空文件 #!/usr/bin/python ...
- k8s pod故障分类与排查
一.Pod故障状态基本有几种Pod状态 处于PendingPod状态 处于WaitingPod状态 处于ContainerCreatingPod状态 ImagePullBackOffPod状态 Cra ...
- HTTP请求头格式和响应格式
HTTP请求头格式 提示: 回车符 \r 换行符 \n 请求首行分析: 请求方式: GET 和 POST 方式: GET请求:地址栏访问.超链接访问都是get请求方式,get请求方式不安全,地址栏大小 ...
- 3.Docker容器学习之新手基础使用
原文地址: http://blog.weiyigeek.top/2019/5/2-docker%E5%AD%A6%E4%B9%A0%E4%B9%8B%E5%9F%BA%E7%A1%80%E4%BD%B ...
- XCTF练习题---MISC---掀桌子
XCTF练习题---MISC---掀桌子 flag:flag{hjzcydjzbjdcjkzkcugisdchjyjsbdfr} 解题步骤: 1.观察题目,发现没有附件,只有一串代码. 2.根据代码内 ...
- XCTF练习题---MISC---gif
XCTF练习题---MISC---gif flag:flag{FuN_giF} 解题步骤: 1.观察题目,下载附件 2.观察下载的附件,发现是由黑白块组成的,试着拼接二维码,好像不太对,再仔细看看感觉 ...
- /proc/meminfo 解释
- [题解] 51 nod 1340 地铁环线
不难看出这是一道差分约束的题目. 但是如果想按照通常的题目那样去建边的话,就会发现这句话--相邻两站的距离至少是1公里--建边后就直接让整个题出现了负环(默认是按求最短路建边),没法做了. 这时我们就 ...
- 踩到一个关于分布式锁的非比寻常的BUG!
你好呀,我是歪歪. 提到分布式锁,大家一般都会想到 Redis. 想到 Redis,一部分同学会说到 Redisson. 那么说到 Redisson,就不得不掰扯掰扯一下它的"看门狗&quo ...
