hdu 1147(线段相交)

Pick-up sticks

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2673    Accepted Submission(s): 975

Problem Description

Stan
has n sticks of various length. He throws them one at a time on the
floor in a random way. After finishing throwing, Stan tries to find the
top sticks, that is these sticks such that there is no stick on top of
them. Stan has noticed that the last thrown stick is always on top but
he wants to know all the sticks that are on top. Stan sticks are very,
very thin such that their thickness can be neglected.

 

Input

Input
consists of a number of cases. The data for each case start with 1 ≤ n ≤
100000, the number of sticks for this case. The following n lines
contain four numbers each, these numbers are the planar coordinates of
the endpoints of one stick. The sticks are listed in the order in which
Stan has thrown them. You may assume that there are no more than 1000
top sticks. The input is ended by the case with n=0. This case should
not be processed.

 

Output

For
each input case, print one line of output listing the top sticks in the
format given in the sample. The top sticks should be listed in order in
which they were thrown.
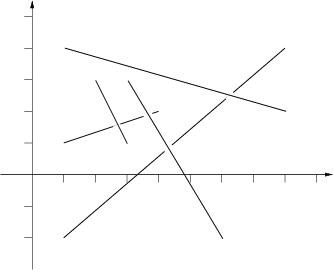
The picture to the right below illustrates the first case from input.

 

Sample Input

5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0

 

Sample Output

Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.

 

题意：n根stick,从第一根开始扔到平面上，第i根有可能覆盖前1-(i-1)的某些stick，求最后还有多少stick没有被覆盖.

 

分析：判断线段是否相交即可。

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int N = ;
struct Point{
    double x,y;
}p[*N];

///叉积
double mult(Point a, Point b, Point c)
{
    return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
}

///a, b为一条线段两端点c, d为另一条线段的两端点 相交返回true, 不相交返回false
bool isCross(Point a, Point b, Point c, Point d)
{
    if (max(a.x,b.x)<min(c.x,d.x))return false;
    if (max(a.y,b.y)<min(c.y,d.y))return false;
    if (max(c.x,d.x)<min(a.x,b.x))return false;
    if (max(c.y,d.y)<min(a.y,b.y))return false;
    if (mult(c, b, a)*mult(b, d, a)<)return false;
    if (mult(a, d, c)*mult(d, b, c)<)return false;
    return true;
}
bool under[N]; ///记录哪些stick在下面
int ans[N];
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF,n){
        memset(under,false,sizeof(under));
        int k=;
        for(int i=;i<=n;i++){
            scanf("%lf%lf%lf%lf",&p[k].x,&p[k].y,&p[k+].x,&p[k+].y);
            k+=;
        }
        for(int i=;i<=n;i++){
            for(int j=i+;j<=n;j++){
                if(isCross(p[*i-],p[*i],p[*j-],p[*j])) {
                    under[i]=true;
                    break;
                }
            }
        }

        printf("Top sticks: ");
        int t=;
        for(int i=;i<=n;i++){
            if(!under[i]) ans[t++]=i;
        }
        for(int i=;i<t-;i++){
            printf("%d, ",ans[i]);
        }
        printf("%d.\n",ans[t-]);
    }
    return ;
}