Logistic Regression学习笔记

1.李航《统计学习方法》；

2.https://blog.csdn.net/laobai1015/article/details/78113214

3.http://www.cnblogs.com/bentuwuying/p/6616680.html

4.http://kyonhuang.top/Andrew-Ng-Deep-Learning-notes/#/Neural_Networks_and_Deep_Learning/神经网络基础

O、逻辑斯蒂回归的缘起

起源于线性回归。线性回归是一种回归分析技术，回归分析本质上就是一个函数值预测的问题，就是找出因变量和自变量之间的关系。回归分析的因变量应是连续变量，若因变量是离散变量，则问题转化为分类问题。

对于给定的数据集，我们需要学习的模型为：

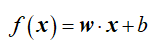
也就是说，我们要从已知的数据集T中学习到模型参数w,b。怎么学呢？

对于给定的样本(x_i,y_i)，我们模型的预测值为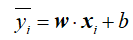，两者之间的误差叫做损失，通常我们采取误差的平方作为损失函数，则在训练数据集T上，模型的损失函数为：

我们的目标是损失函数最小化，即：

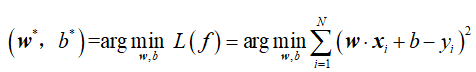
上述这最后一步怎么求？我们可以用梯度下降法来求解上述最小化问题的数值解。关于梯度下降法，请参考：梯度下降原理及Python实现，和梯度下降（Gradient Descent）小结

以上是线性回归(Linear Regression)，其“线性”二字的内涵在于它认为模型输出(y)是模型输入(x)的线性表达式。而且，线性模型也可以用于分类！

考虑二分类问题，我们有训练数据集，我们需要一个模型，能够告诉我们P(y|x)。比如，这个模型告诉我们P(y=1|x₁)=0.6，P(y=0|x₁)=0.4，然后因为0.6>0.4，所以模型认为特征x₁对应的预测值y为1.如何找到这个模型呢？

借用线性模型的思想，我们引入w,b，由于w·x+b取值是连续的，所以它不能拟合离散变量y（取值为0或1），但可以用它拟合同为连续变量的条件概率P(y=1|x)。

我们注意到，w·x+b取值范围是-∞~+∞，不符合概率取值范围0~1，因此得将w·x+b进行转换，使其映射到0~1的范围。函数可以实现转换，最理想的是单位阶跃函数：

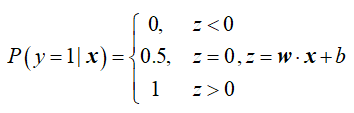
但是阶跃函数不满足单调可导，也就不能用梯度下降法求解损失函数最小化的参数w,b。我们可以找一个可导、与阶跃函数形状相似的函数，对数概率函数(logistic function)就是这样一个替代函数：，该函数也称sigmoid函数，该函数具有如下的特性：当x趋近于负无穷时，y趋近于0；当x趋近于正无穷时，y趋近于1；当x=1/2时，y=0. 可参考：http://www.cnblogs.com/maybe2030/p/5678387.html

一、逻辑斯蒂回归的概览

1.逻辑斯蒂回归是一种分类算法，最常用的二项逻辑斯蒂回归只适用于二分类问题；

2.逻辑斯蒂回归算法的思想就是：假定一件事情发生(Y=1)的对数几率是特征(x)的线性函数。或者说，在逻辑斯蒂回归模型中，输出Y=1的对数几率是由输入x的线性函数表示的。

3.二项逻辑斯蒂回归模型定义：

二项逻辑斯蒂回归模型是如下的条件概率分布：

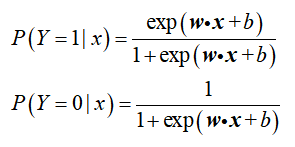
说明：上述两个式子代表了所有逻辑斯蒂回归模型的通用表达式，具体模型之间的差别在于模型参数w和b。对于给定的输入实例x，按照上述两式可以求得P(Y=1|x)和P(Y=0|x)。逻辑斯蒂回归比较两个条件概率值的大小，将实例x分到概率值较大的那一类。

4.Logistic 回归可以看作是一个非常小的神经网络。下图是一个典型例子：（参考文献4）

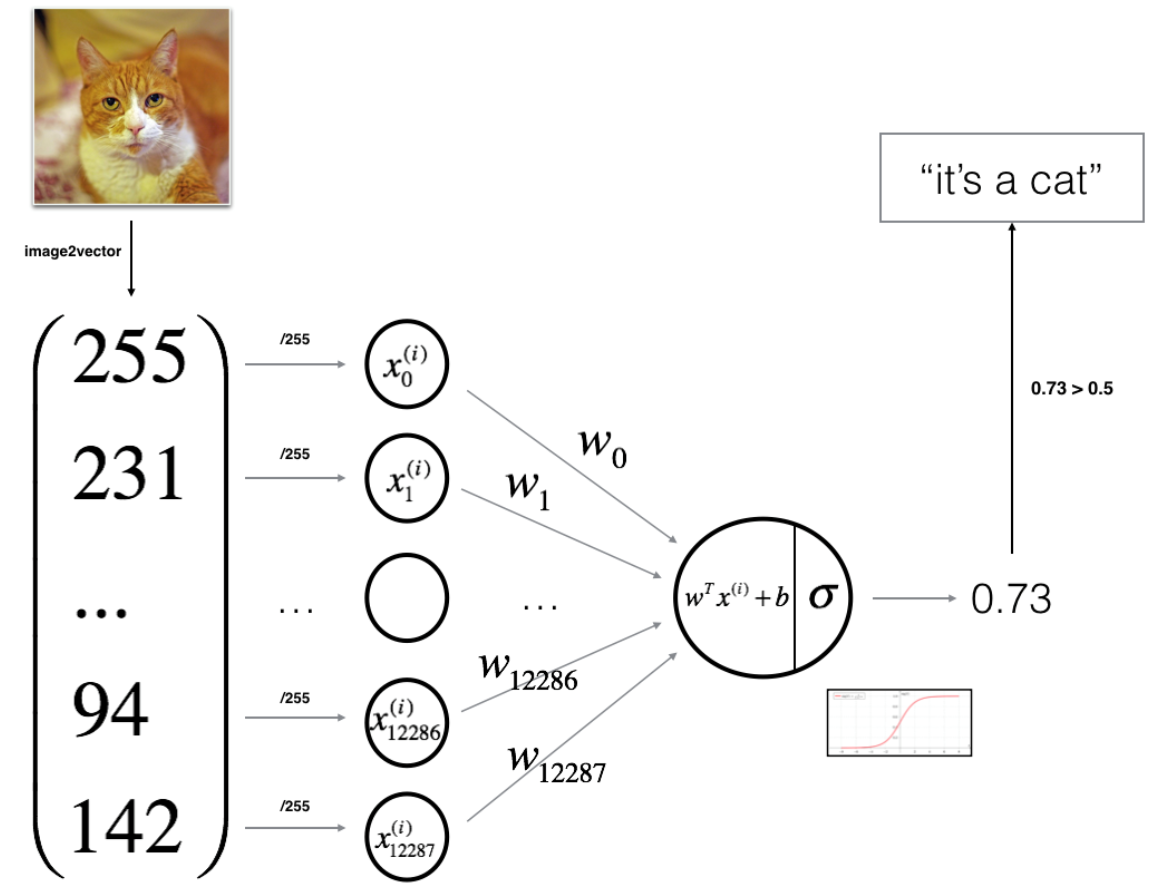
二、逻辑斯蒂回归的流程

我们要使用逻辑斯蒂回归模型搭建一个分类器，首先得写出这个逻辑斯蒂回归模型，其次得写出模型好坏的评价函数（即代价函数cost function），最后是估计模型的参数w（b被融入到w中，即取w₀=b，且将偏置项的变量x₀设置为1）——即最小化损失函数来求得参数w。

1.对于给定的训练数据集，首先我们初始化一个模型w，认为

。

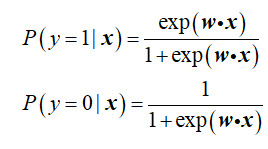显然对于训练数据(x_i,y_i)，最好的模型是能够给出P(y=1|x_i)=1,P(y=0|x_i)=0这样的预测，显然这是不容易的。同时，由于我们一共有m条训练数据，我们必须要找到这样的模型，使得模型对全部训练数据集的整体预测效果最佳。

2.如何评价模型好坏？直观地理解就是比较各个训练样本的真实标签和模型预测标签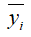之间的误差值的加总，而这个总误差不便于求导。因此我们另外从极大似然估计的角度去描述模型好坏，即使得所有训练数据最有可能发生的模型w，就是我们要找的模型。（摘自参考资料2）

因此得到：

................................(*)

3.最后就是最小化J(θ)，逻辑斯蒂回归学习中通常采用的方法是梯度下降法和牛顿法。参考文献3。

对上述(*)式的J(θ)求θ的导数，可得：

根据梯度下降法，得到如下的更新公式：

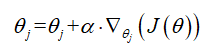
三、总结

以上的1步就是给出逻辑斯蒂回归这一模型认为的判别函数集（模型参数未定，所以是一个函数集），第2步就是给出损失函数，就是给出了判断函数好坏的标准，第3步就是最小化损失函数来求得模型参数，就是挑选最好的函数的过程。