[Atcoder Grand Contest 002] Tutorial

Link:

A:

……

#include <bits/stdc++.h>

using namespace std;

int a,b;

int main()

{

    scanf("%d%d",&a,&b);

    if(a>) puts("Positive");

    else if(a<=&&b>=) puts("Zero");

    else if((b-a)&) puts("Positive");

    else puts("Negative");

    return ;

}

Problem A

B:

分别用$cnt[i]$和$ok[i]$记录当前的个数以及是否可能计入答案

注意模拟时用$ok[x[i]]$来更新$ok[y[i]]$

#include <bits/stdc++.h>

using namespace std;

const int MAXN=1e5+;

int n,m,x,y,cnt[MAXN],ok[MAXN],res;

int main()

{

    scanf("%d%d",&n,&m);

    ok[]=;

    for(int i=;i<=n;i++) cnt[i]=;

    for(int i=;i<=m;i++)

    {

        scanf("%d%d",&x,&y);

        cnt[x]--;cnt[y]++;

        if(ok[x]) ok[y]=true;

        if(ok[x]&&!cnt[x]) ok[x]=false;

    }

    for(int i=;i<=n;i++) res+=ok[i];

    printf("%d",res);

    return ;

}

Problem B

C:

又是一道构造题……

遇到输出Possible/Impossible的题目先想一想Impossible的条件是什么

对于此题，明显如果没有$dat[i]+dat[i+1]\ge L$则无解

那么有解时从两边一路断到中间即可

#include <bits/stdc++.h>

using namespace std;

int n,l,pos,a,b;

int main()

{

    scanf("%d%d%d",&n,&l,&a);

    for(int i=;i<=n;i++)

    {

        b=a;scanf("%d",&a);

        if(a+b>=l) pos=i-;

    }

    if(!pos) return puts("Impossible"),;

    puts("Possible");

    for(int i=;i<=pos-;i++) printf("%d\n",i);

    for(int i=n-;i>=pos;i--) printf("%d\n",i);

    return ;

}

Problem C

D:

整体二分+并查集合并

等把整体二分和cdq分治学好了再来填吧……

E:

题面大意：

有$n$堆石子，每次可以选择取一整堆或选择每堆取一个

取到最后一个石子的人判负

在本蒟蒻看来是博弈里的神题了

将每堆石子按照从多到少排序后，可以发现每进行一次操作，其实就是去掉一整行或一整列

（类似于杨氏矩阵查找时的操作）

最后没有石子时下一次操作的人获胜

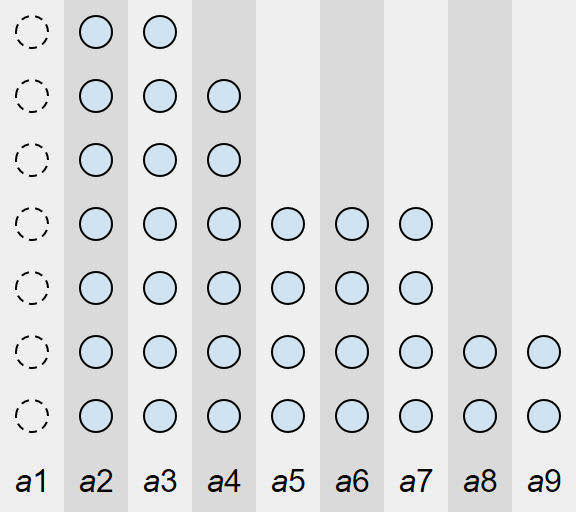
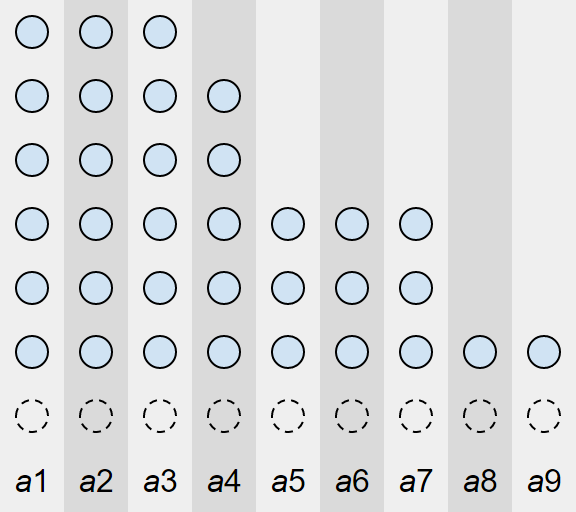
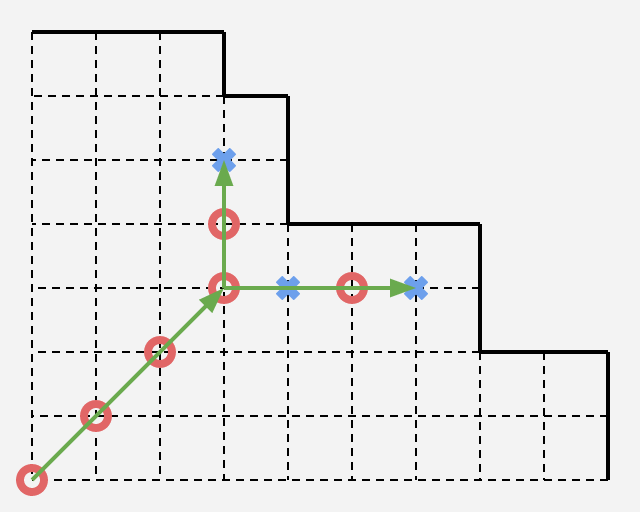
因此可以将模型转化为有关路径的模型：

每个人每次可以将起始点向上或向右移动一次，将点移出边界的人判负

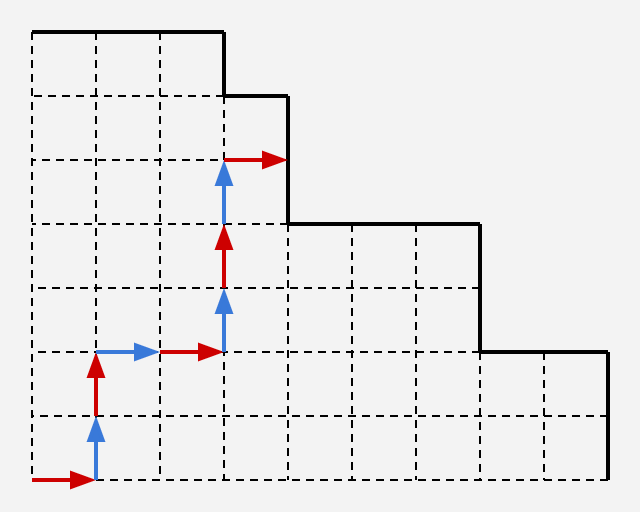
接下来推断必胜态和必败态即可：

1、在边界外的一圈都是必胜态

2、根据必败态的定义，对于状态$(x,y)$，如果$(x,y+1),(y,x+1)$均为必胜态则$(x,y)$为必败态

3、根据必胜态的定义，对于状态$(x,y)$，如果$(x,y+1),(y,x+1)$存在必败态则$(x,y)$为必胜态

由此推出起点$(1,1)$的状态：

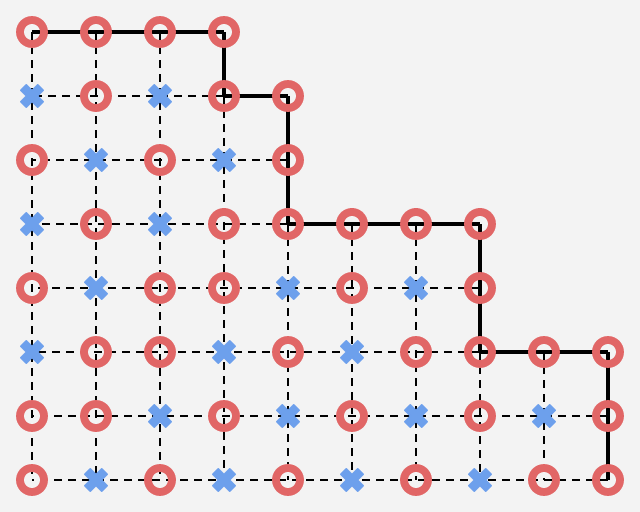
但$\sum_{i=1}^n a_i$的复杂度不满足要求

通过打表找规律可知：每一条斜率为1的直线上的状态相同

因此除了边界外，不在直线$y=x$上的状态是无关紧要的

于是我们找到$y=x$能延伸到的最远点，设其到上边界距离为$d_i$，到右边界距离为$d_j$

当且仅当$d_i$和$d_j$均为偶数时$(1,1)$为必败态，否则为必胜态。模拟即可

#include <bits/stdc++.h>

using namespace std;

int n,dat[];

bool cmp(int a,int b){return a>b;}

int main()

{

    scanf("%d",&n);

    for(int i=;i<=n;i++) scanf("%d",&dat[i]);

    sort(dat+,dat+n+,cmp);

    int row=,col=;

    while(dat[row+]>=row+) row++;

    while(dat[row+col+]>=row) col++;

    printf(!((dat[row]-row)&)&&!(col&)?"Second":"First");

    return ;

}

Problem E

能总结的思路还是比较多的：

1、对同类操作的合并

同类操作最好能统一处理

通过排序等方式将对每堆进行的总共$n$次操作化为一次操作

2、可以将博弈论问题转化成点的移动模型

由于要确定必胜/必败态，最好能将每一个状态简化，那么点的位置自然是最好表示的状态

3、打表找规律

很多博弈论问题为了简化$SG$函数都要打表找规律，算是要经常用的常规操作

F:

可以先通过有序化来简化问题：

钦定第$i$个0来自于第$i$中颜色，最后的结果乘上$n!$就行了

（可以将颜色序列$1,2,3....n$想成每次用$a_1,a_2,a_3.....a_n$去替换）

此时发现序列要满足：

1、第一个颜色$i$要出现在第$i$个0之后（保证合法性）

2、第一个颜色$i$要出现在第一个颜色$i-1$之后（保证有序性，否则会重复计算）

接下来直接上各种$dp$就行了，维护已有的0的个数和已处理的颜色数

官方题解提供了一种值得借鉴的思路：

由于颜色的有序性，将模型转化为求建图后拓扑排序的方案数

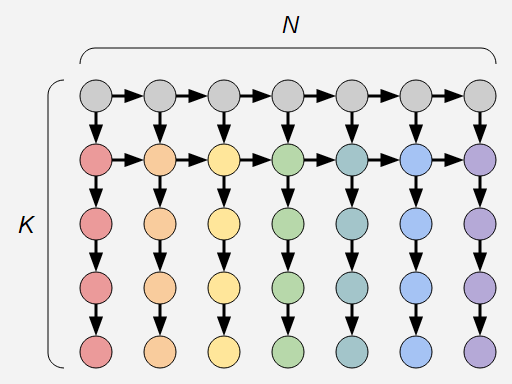
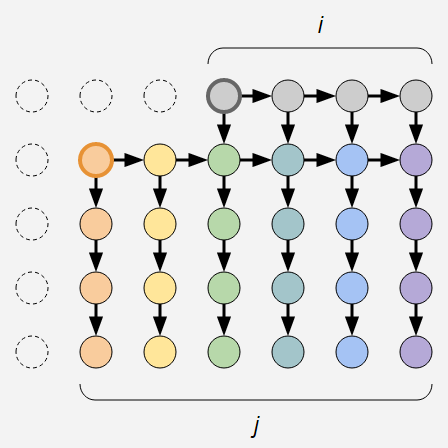
接下来从后往前，令$dp[i][j]$为已有$i$个0，确定了后$j$种颜色的方案数进行$dp$

分两种情况统计：$dp[i][j]=dp[i-1][j]+dp[i][j-1]*C_{i+(k-1)*j-1}^{k-2} (j>i)$

心情好用滚动数组优化下空间

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int MAXN=,MOD=1e9+;

int n,k,fac[MAXN*MAXN],inv[MAXN*MAXN],dp[MAXN];

ll quick_pow(ll a,ll b)

{

    ll ret=;

    for(;b;b>>=,a=a*a%MOD)

        if(b&) ret=ret*a%MOD;

    return ret;

}

ll C(int a,int b)

{if(a<b) return ;return 1ll*fac[a]*inv[a-b]%MOD*inv[b]%MOD;}

void inc(int &a,int b){a+b>MOD?a+=b-MOD:a+=b;}

int main()

{

    scanf("%d%d",&n,&k);

    if(k==) return puts(""),;

    fac[]=dp[]=;

    for(int i=;i<=n*k;i++) fac[i]=1ll*fac[i-]*i%MOD;

    inv[n*k]=quick_pow(fac[n*k],MOD-);

    for(int i=n*k-;i>=;i--) inv[i]=1ll*inv[i+]*(i+)%MOD;

    for(int i=;i<=n;i++)

        for(int j=i+;j<=n;j++)

            inc(dp[j],dp[j-]*C(i+(k-)*j-,k-)%MOD);

    ll res=1ll*dp[n]*fac[n]%MOD;

    printf("%lld",res);

    return ;

}

Problem F

1、如果不同颜色具有可替代性，构造有序性来简化问题和思维难度

2、有序性 $<->$ 拓扑排序

3、线性求阶乘逆元、对加法取模优化

用了好几次了，记得套路就行……