bzoj 2566 calc 拉格朗日插值

calc

Time Limit: 30 Sec  Memory Limit: 512 MB
Submit: 377  Solved: 226
[Submit][Status][Discuss]

Description

　　一个序列a1,...,an是合法的，当且仅当：
　　长度为给定的n。
　　a1,...,an都是[1,A]中的整数。
　　a1,...,an互不相等。
　　一个序列的值定义为它里面所有数的乘积，即a1a2...an。
　　求所有不同合法序列的值的和。
　　两个序列不同当且仅当他们任意一位不一样。
　　输出答案对一个数mod取余的结果。

Input

　　一行3个数，A，n，mod。意义为上面所说的。

Output

　　一行结果。

Sample Input

9 7 10007

Sample Output

3611

HINT

数据规模和约定

　　0:A<=10,n<=10。

　　1..3:A<=1000,n<=20.

　　4..9:A<=10^9,n<=20

　　10..19:A<=10^9,n<=500。

　　全部:mod<=10^9,并且mod为素数，mod>A>n+1

Source

不得不说dp设的也是十分好的，估计自己还想不出。

f[i][j]表示，前i个元素中，选择了j个的方案数，这个转移是怎么样的呢？

f[i][j]=f[i-1][j-1]*i*j+f[i-1][j]，这个转移中的第二个十分显然，第一个是什么意思，就是选择了i这个元素，

插入到j中的任意一个位置，就是j个位置离随便哪个位置都可以，然后根据乘法的分配律，结合一下，就可以了。

当然j可以大于i，就因为i可以插到后面的位置。

就算想出了这一步，下面发现这个表是一个几次的多项式我基本上不可能会发现

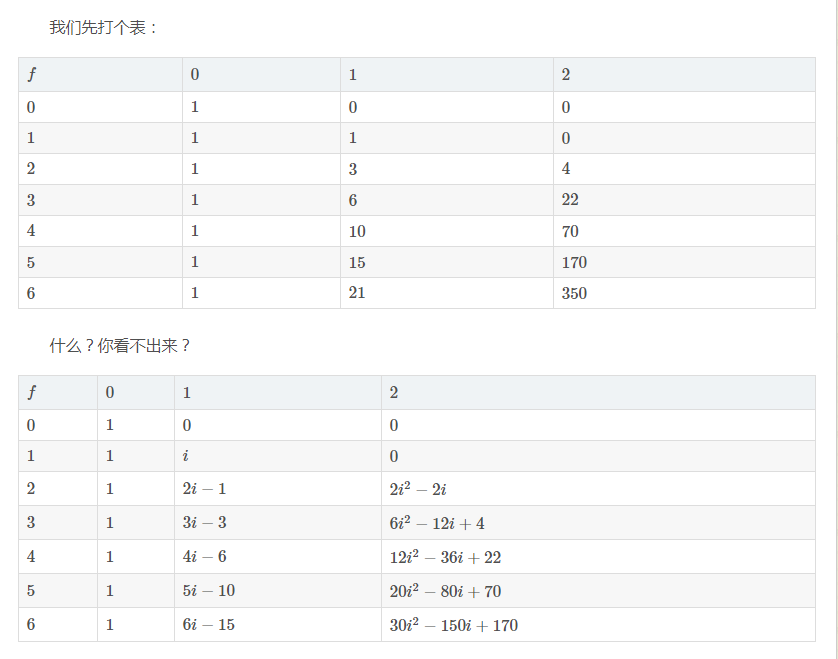
某大佬打了这个表，然后这个多项式怎么搞出来的真的有点厉害

但是这个多项式是没用的，因为这个多项式的系数是变化的，所以没有什么用

有没有一个多项式的系数是不变的呢？
然后就有大佬发现了

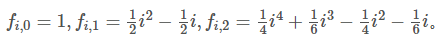
发现了这个，即f[i][j]的系数只和j有关，是一个最高项系数是2*j的多项式，然后就稳了，

这样只需要求出2*n+1个点就可以插值了，朗格朗日插值求一下m这个位置的值即可。

 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<iostream>
 #include<algorithm>

 #define N 1007
 #define ll long long
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(!isdigit(ch)){if(ch=='-')f=-;ch=getchar();}
     while(isdigit(ch)){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }

 int n,m;
 ll p,ans;
 ll f[N][N];

 ll fast_pow(ll a,ll b)
 {
     ll ans=;
     while(b)
     {
         if (b&) (ans*=a)%=p;
         (a*=a)%=p;
         b>>=;
     }
     return ans;
 }
 void Lagrange()
 {
     for (int i=;i<=*n;i++)
     {
         ll s1=,s2=;
         for (int j=;j<=*n;j++)
             if (j!=i)
             {
                 (s1*=(m-j))%=p;
                 (s2*=(i-j))%=p;
             }
         (ans+=f[i][n]*s1%p*fast_pow(s2,p-)%p)%=p;
     }
 }
 int main()
 {
     m=read(),n=read(),p=read();
     f[][]=;
     for (int i=;i<=*n;i++)
     {
         f[i][]=f[i-][];
         for (int j=;j<=n;j++)
             f[i][j]=(f[i-][j-]*i%p*j+f[i-][j])%p;
     }
     if (m<=*n)
     {
         printf("%lld\n",f[m][n]);
         return ;
     }

     Lagrange();
     ans=(ans%p+p)%p;

     printf("%lld\n",ans);
 }