【总结整理】webGIS学习thinkGIS（四）WebGIS中通过行列号来换算出多种瓦片的URL 之离线地

http://www.thinkgis.cn/topic/541a5319da8db186fd06e097

1.前言

在前面我花了两个篇幅来讲解行列号的获取，也解释了为什么要获取行列号。在这一章，我将把常见的几种请求瓦片时的URL样式罗列出来，并且给出大致的解释。我在这里将地图分为离线地图和在线地图。所谓离线地图，即保存在本地而没有发布的地图。在线地图即发布与网上，可以通过浏览器访问的地图。

2.ArcGIS切图——exploded类型

在前面章节中我已经贴出了exploded类型的切图图片，这里再次给出。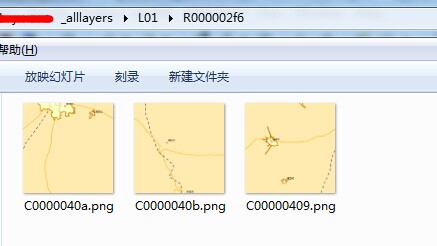

那么如何通过行列号来换算出此瓦片的URL呢。我们首先可以通过观察得出三个结论：

（1）L开头的代表了Level，R开头的代表了row，C开头的代表了Col。

（2）确定这个后，我们再继续观察，可以发现L后的数字是两位字符串，R后的是八位字符串，C后的也是八位字符串。

（3）英文后的数字均是16进制数，然后不足位数的用0补充。

我想大家在知道了这三个结论后，通过行列号来获得离线松散瓦片的地址该不难了吧，我们只需把级别、行列号换算成16进制后，不足位数的再用0补位，最后加上英文标识，于是这个瓦片的地址也便可以额找到了。

3.ArcGIS 切图——bundle类型

这里我也首先贴出这种瓦片类型的样式：

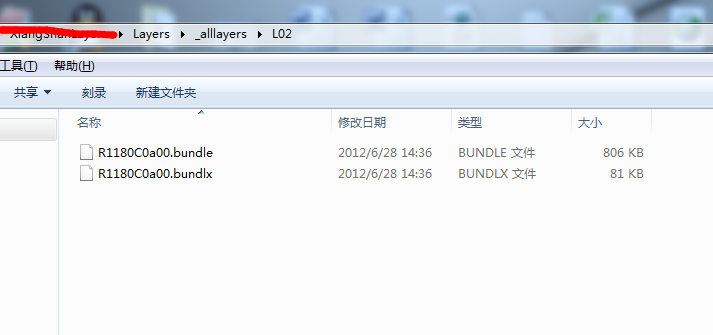
这个瓦片的获取咋一看确实是毫无头绪，因为arcgis的这种紧凑型格式将图片进行了包装，并不能直观的看到图片。ArcGIS号称这种格式目前是不公开解析方法的，并且同样在网上也很难收到对应的解析方法。但是，我的一个很有想法的同事，在去年时花了些时间后已经将这种格式下的瓦片获取方法破解了，并且我们已经成功运用到多个项目中。

这里我就只给出几个提示吧，根据我的这几个提示，我想读者只要再加一把劲一定可以破解的：

（1）同样，L、R、C后的是地图的级别、行号、列号。

（2）R、C后的字符串固定是4位。

（3）R、C后的数字是通过行列号除以128后再转成16进制，然后将不足的位数补零。

（4）Bundle文件中存放的是图片二进制流，BundleX文件中存放的是对应瓦片在Bundle中的地址，是一个索引文件。

（5）然后……

然后就是如何在索引文件中找到应该读取的地方，获得瓦片在Bundle中所在的地址后，再去Bundle中的相应地址里读取图片。不过，这里补充一下，Bundle中也不是只有瓦片的，它里面还包含了每个瓦片的大小，也就是你读这个瓦片需要读取多少个二进制的数目。

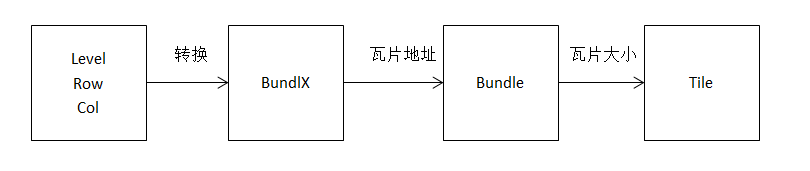
这里再次感谢我的同事的智慧的结晶，否则这篇文章一定是不完整的。

不是只有瓦片的，它里面还包含了每个瓦片的大小，也就是你读这个瓦片需要读取多少个二进制的数目。

4.非常见瓦片格式——国土局的瓦片

在我们项目中经常可以见到非ArcGIS的瓦片系列，比如超图的、中地的等等。这里我给出某国土局的瓦片格式，其实目前很多国土局自己的瓦片均是这个组织格式。

同样我先给出瓦片的样式图：

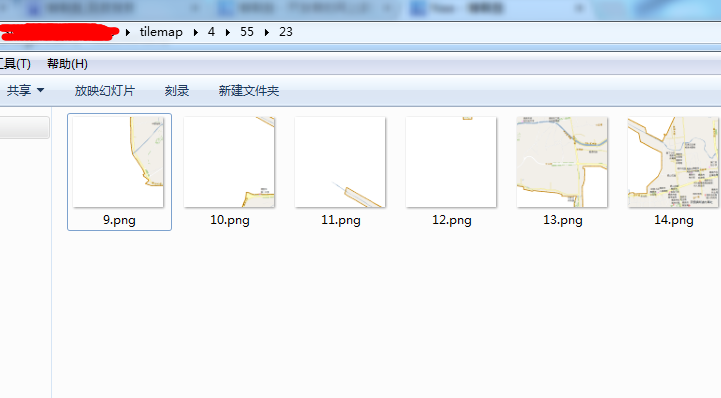
大家是不是很奇怪，明明该是三个层次的呀，Level、Row、Col的呀，怎么这个就有四个层次呢。是的，国土局的瓦片中除了这三个参数外，还有一个FileID参数。

这里我直接给出换算公式：

FixedLevel=Level;

FixedRow=Math.floor(Row/4);

FixedCol=Math.floor(Col/4);

FileID=(Row)%4)+ 4*((Col)%4);

其URL的地址就是\FixedLevel\FixedRow\FixedCol\FileID.png。

5.总结

在这一节里我们针对两种常见离线地图格式和一种特殊的离线地图格式进行了解析。从这个解析中我们可以看出，不管是什么地图，行列号都是必须的条件。所以对行列号如何得到还不是很清楚的读者，请将我这个系列中的第二节和第三节再次专心的读一遍，相信你和我一样一定有不一样的收获的。

下一节里，我们将对在线的地图的URL解析进行讲解，在线的地图的URL获取相对简单。我们同样会对符合OGC标准的在线地图以及特殊的在线地图服务进行分析。欢迎持续关注。