Codeforces 460 D. Little Victor and Set

暴力+构造

If r - l ≤ 4 we can all subsets of size not greater than k.
Else, if k = 1, obviously that answer is l. If k = 2,
answer is 1, because xor of numbers 2x and 2x + 1 equls 1.
If k ≥ 4 answer is 0 because xor of
to pairs with xor 1 is 0.

If k = 3, we can choose numbers 2x and 2x + 1 with xor 1.
So we need to know, if we can get xor equals 0. Suppose that
there are 3 such numbers x, y and z (r ≥ x > y > z ≥ l)
with xor equals 0. Consider the most non-zero bit of numberx.
At the same bit of y it's also 1, because xor equls
0, and y > z. Consider the next bit of numbers. If z have 0 there,
we have to do next: set the previous bit of numbers x and y equals 0,
and set current bit equals 1. Obviously xor still equals
0, z hadn't changed and numbers x and y stood
closer to z, so they are still at [l, r].And x > y.Consider
the next bit of numbers. If z has zero here than we will change most bits of x и y at
the same way and so on. z > 0, so somewhen we will get to bit in which z has 1.
Since xorequals 0, the same bit of x would
be 1 because x > y, and y would
have 0 there. At the next bits we will change bit in x to 0,
and in numbers y and z to 1.Finally z would
be greater or equal than before, and x would be less or greater than before, and x > y > z would
be correct. So, we have the next: if such numbers x, y and z exist
than also exist numbers:

1100…000

1011…111

0111…111

with xor equals 0. There are not much such triples, so we
can check them.

D. Little Victor and Set

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Victor adores the sets theory. Let us remind you that a set is a group of numbers where all numbers are pairwise distinct. Today Victor wants to find a set of integers S that
has the following properties:

• for all x 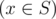 the
  following inequality holds l ≤ x ≤ r;
• 1 ≤ |S| ≤ k;
• lets denote the i-th element of the set S as si;
  value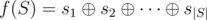  must
  be as small as possible.

Help Victor find the described set.

Input

The first line contains three space-separated integers l, r, k (1 ≤ l ≤ r ≤ 1012; 1 ≤ k ≤ min(106, r - l + 1)).

Output

Print the minimum possible value of f(S). Then print the cardinality of set |S|.
Then print the elements of the set in any order.

If there are multiple optimal sets, you can print any of them.

Sample test(s)

input

8 15 3

output

1
2
10 11

input

8 30 7

output

0
5
14 9 28 11 16

Note

Operation 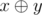 represents
the operation of bitwise exclusive OR. In other words, it is the XOR operation.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long int LL;

LL L,R,K;
LL ans=0x3f3f3f3f3f3f3f3f;

int main()
{
    cin>>L>>R>>K;
    if(R-L+1<=4)
    {
        LL m=R-L+1;
        LL sig=0;
        for(LL i=1;i<(1LL<<m);i++)
        {
            LL temp=0;
            LL wei=0;
            LL si=i;
            while(si)
            {
                wei++;
                si=si&(si-1);
            }
            if(wei>K) continue;
            for(LL j=0;j<m;j++)
            {
                if(i&(1LL<<j))
                {
                    temp^=L+j;
                }
            }
            if(temp<ans)
            {
                ans=temp;
                sig=i;
            }
        }
        cout<<ans<<endl;
        LL wei=0;
        LL tsig=sig;
        while(tsig)
        {
            wei++;
            tsig=tsig&(tsig-1);
        }
        cout<<wei<<endl;
        for(LL i=0;i<m;i++)
        {
            if(sig&(1<<i))
            {
                cout<<L+i<<" ";
            }
        }
        cout<<endl;
    }
    else
    {
        if(K==1)
        {
            cout<<L<<endl;
            cout<<1<<endl;
            cout<<L<<endl;
        }
        else if(K==2)
        {
            if(L%2) L++;
            cout<<1<<endl;
            cout<<2<<endl;
            cout<<L<<" "<<L+1<<endl;
        }
        else if(K==3)
        {
            bool flag=false;

            LL mx=3,mi=1;
            while(mx<=R)
            {
                if(mi>=L)
                {
                    flag=true;
                    cout<<0<<endl<<3<<endl;
                    cout<<mx<<" "<<mx-1<<" "<<mi<<endl;
                    break;
                }

                mx<<=1LL;
                mi<<=1LL; mi++;
            }

            if(flag==false)
            {
                if(L%2) L++;
                cout<<1<<endl;
                cout<<2<<endl;
                cout<<L<<" "<<L+1<<endl;
            }
        }
        else
        {
            cout<<0<<endl;
            cout<<4<<endl;
            if(L%2) L++;
            cout<<L<<" "<<L+1<<" "<<L+2<<" "<<L+3<<endl;
        }
    }
    return 0;
}