联赛模拟测试22 B. 分组配对 倍增+二分

题目描述

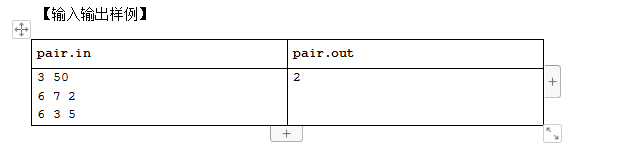
分析

首先,容易发现一个小组内的最优配对方式(能得到最大综合实力的方式)

一定是实力值最大的男生和最大的女生配对,次大的和次大的配对,以此类推.

但是每次新插入一个值时，需要用 \(nlogn\) 的时间复杂度去维护这个最大实力值

如果暴力去扩展时间效率是无法接受的

然后我们会发现答案具有单调性，可以枚举一个左区间，然后二分查找右区间

但是当遇到每一组的人数很小的情况时，二分会被卡成 \(n^2 logn\)

因此我们需要先用倍增处理出二分的区间

在处理出的区间里进行二分查找

这样,当实际组大小是\(k\)时,时间复杂度应为\(O(klog^2k)\)

则总时间复杂度不超过\(O(nlog^2n)\)

代码

#include<cstdio>
#include<set>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
#define rg register
inline int read(){
	rg int x=0,fh=1;
	rg char ch=getchar();
	while(ch<'0' || ch>'9'){
		if(ch=='-') fh=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9'){
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return x*fh;
}
const int maxn=5e5+5;
int n,a[maxn],b[maxn],cnt,c[maxn],d[maxn];
long long m;
bool jud(int l,int r){
	rg long long nans=0;
	rg int ncnt=0;
	for(rg int i=l;i<=r;i++){
		c[++ncnt]=a[i];
		d[ncnt]=b[i];
	}
	std::sort(c+1,c+1+ncnt);
	std::sort(d+1,d+1+ncnt);
	for(rg int i=1;i<=ncnt;i++){
		nans+=1LL*c[i]*d[i];
	}
	return nans<=m;
}
int main(){
	n=read();
	scanf("%lld",&m);
	for(rg int i=1;i<=n;i++){
		a[i]=read();
	}
	for(rg int i=1;i<=n;i++){
		b[i]=read();
	}
	rg int head=1,now=0;
	while(head<=n){
		cnt++;
		now=0;
		while(1){
			if(head+(1<<now)-1>n || !jud(head,head+(1<<now)-1)) break;
			now++;
		}
		rg int nl=head+(1<<(now-1))-1,nr=head+(1<<(now))-1,nmids;
		nr=std::min(n,nr);
		while(nl<=nr){
			nmids=(nl+nr)>>1;
			if(jud(head,nmids)) nl=nmids+1;
			else nr=nmids-1;
		}
		head=nr+1;
	}
	printf("%d\n",cnt);
	return 0;
}