题解-[NOI2005]瑰丽华尔兹

题解-[NOI2005]瑰丽华尔兹

[NOI2005]瑰丽华尔兹

\(n\times m\) 的矩阵。以 \((x,y)\) 为起点。一共 \(k\) 段时间，每段时间为 \([s_i,t_i](t_i+1=s_{i+1})\)，每秒可以向 \(d_i\) 方向运动一个单位（不能超出矩阵，不能走到给出矩阵的障碍物处，\(d=\{1,2,3,4\}\) 分别表示上下左右）或不动，求最后运动最长总距离。

数据范围：\(1\le n,m\le 200\)，\(1\le k\le 200\)，\(1\le s_i\le t_i\le 4\times 10^4\)。

---

非常引人入胜的一道题，表明上很毒瘤，其实故事情节生动，题目做法巧妙，代码长而不烦。完美啊！连我这个小蒟蒻都一次过了，除了在 \(\texttt{vector}\) 开队列大小上出了点小问题。

---

很明显可以 \(\texttt{dp}\)：

\(f_{w,i,j}\) 表示第 \(w\) 段时间，走到 \((i,j)\) 这个格子时的最长路长度。

\(f_{w,i,j}\) 可以由 \(f_{w-1,i',j'}\) 推得。

如果直接野蛮递推（暴力找同行（列）的 \(i'\) 或 \(j'\)），时间复杂度为 \(\Theta(knm(n+m))\) 稳炸。

考虑到递推时的单向性和单调性，想到可以用单调队列。

---

对于每个 \(w\)，\(d_w\) 不同，所以可以分类讨论不同方向时的 \(\texttt{dp}\) 递推方法。

举例：假设 \(d_w=4\)，即方向为右。

因为是横向递推的，所以可以单独考虑每一行。

怎么用单调队列呢？

1. 队列中存的是当前格左端 从头到尾 期望贡献单调递减的 列下标。
2. 清空 \(w\) 时间段长度内不可达到的或与当前格被障碍物隔绝的列下标。
3. 遍历列的同时维护单调队列并求得 \(f_{w,i,j}\) 递推值。

这东西好想却难讲，于是蒟蒻画了个图：

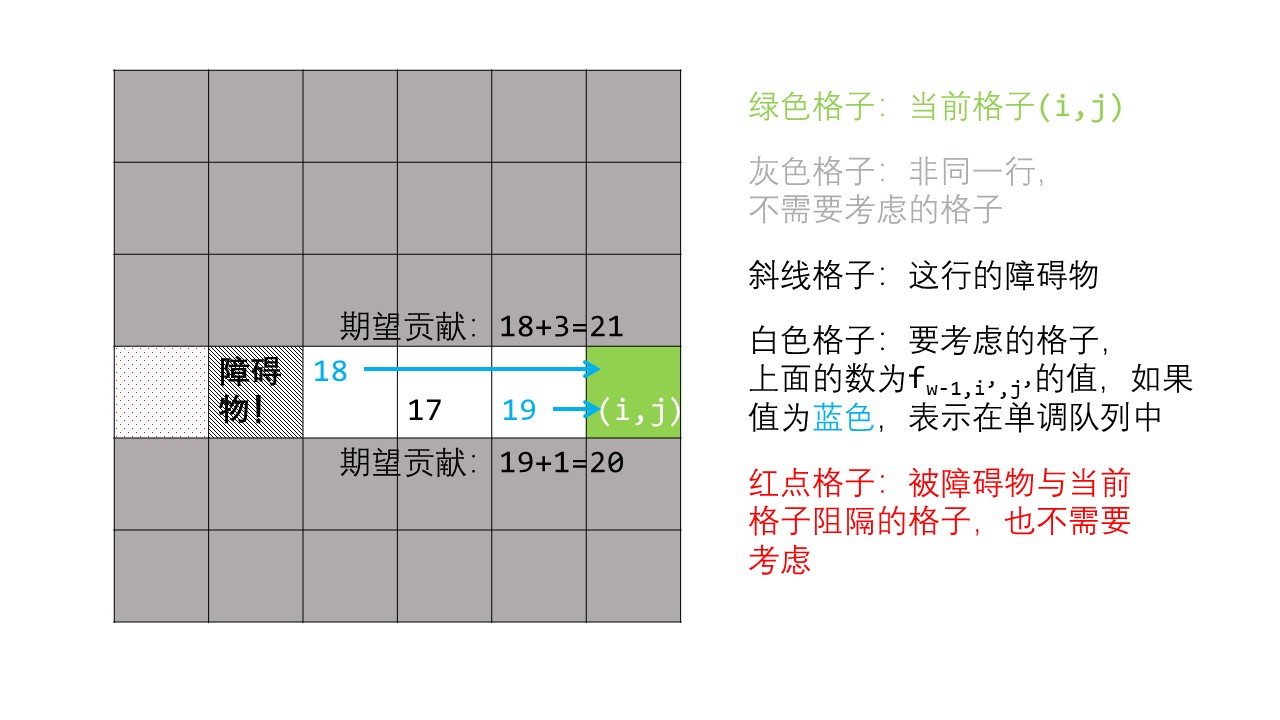
其实绿色格子上也应该有数字，也应该考虑是否放进单调队列，但是那样问题会稍微复杂一些。

设单调队列的头为 \(qtop\)，如上图中 \(queue=\{3,5\}\)，\(qtop=3\)。

所以递推转移方程为：

\[f_{w,i,j}=f_{w,qtop}+j-qtop
\]

所以上图中：

\[f_{w,4,6}=f_{w-1,4,3}+6-3=21
\]

所以当 \(d_w=4\) 时的代码：

for(re int i=1;i<=n;i++){
	l=1,r=0;
	for(re int j=1;j<=m;j++){
		if(G[i][j]){l=r+1;continue;} //如果遇到障碍物，清空数组
		while(l<=r&&q[l]<j-mv.se) l++; //把该时间段走不到的排除（时间太少了）
		while(l<=r&&f[p^1][i][q[r]]-q[r]<=f[p^1][i][j]-j) r--; //维护队列期望贡献单调递减
		q[++r]=j,f[p][i][j]=max(f[p][i][j],f[p^1][i][q[l]]+j-q[l]); //队列加入j，一路递推dp
	}
}

至于另外 \(3\) 个方向，自己拿纸笔模拟模拟即可知。

---

代码实现的时候，其实 \(w\) 这一维可以用滚动数组优化到 \(\Theta(1)\)。

总时间复杂度为 \(\Theta(knm)\)，空间复杂度为 \(\Theta(nm)\)。

---

Code

#include <bits/stdc++.h>
using namespace std;

//Start
#define re register
#define il inline
#define mk make_pair
#define mt make_tuple
#define pb push_back
#define db double
#define lng long long
#define fi first
#define se second
const int inf=0x3f3f3f3f;

//Data
const int N=200;
int n,m,x,y,k,G[N+7][N+7];
vector<pair<int,int>> Mv;
int f[2][N+7][N+7];
char s[N+7];

//Main
int main(){
	scanf("%d%d%d%d%d",&n,&m,&x,&y,&k);
	for(re int i=1;i<=n;i++){
		scanf("%s",s+1);
		for(re int j=1;j<=m;j++) G[i][j]=(s[j]=='x');
	}
	for(re int i=1,s,t,d;i<=k;i++){
		scanf("%d%d%d",&s,&t,&d);
		Mv.pb(mk(d,t-s+1)); // 重要的是时间段长度
	}
	re int p=0,l,r;
	re vector<int> q(max(n,m)+7);
	//我原来这里竟然写成了 re vector<int> q(n+7);，如果 n<m 就 RE 了
	for(re int i=1;i<=n;i++)
		for(re int j=1;j<=m;j++) f[p][i][j]=-inf;
	f[p][x][y]=0;
	for(re auto mv:Mv){
		p^=1; //滚动
		for(re int i=1;i<=n;i++)
			for(re int j=1;j<=m;j++) f[p][i][j]=-inf;
		if(mv.fi==1){ // 上
			for(re int j=1;j<=m;j++){
				l=1,r=0;
				for(re int i=n;i>=1;i--){
					if(G[i][j]){l=r+1;continue;}
					while(l<=r&&q[l]>i+mv.se) l++;
					while(l<=r&&f[p^1][q[r]][j]+q[r]<=f[p^1][i][j]+i) r--;
					q[++r]=i,f[p][i][j]=max(f[p][i][j],f[p^1][q[l]][j]+q[l]-i);
				}
			}
		} else if(mv.fi==2){ // 下
			for(re int j=1;j<=m;j++){
				l=1,r=0;
				for(re int i=1;i<=n;i++){
					if(G[i][j]){l=r+1;continue;}
					while(l<=r&&q[l]<i-mv.se) l++;
					while(l<=r&&f[p^1][q[r]][j]-q[r]<=f[p^1][i][j]-i) r--;
					q[++r]=i,f[p][i][j]=max(f[p][i][j],f[p^1][q[l]][j]+i-q[l]);
				}
			}
		} else if(mv.fi==3){ // 左
			for(re int i=1;i<=n;i++){
				l=1,r=0;
				for(re int j=m;j>=1;j--){
					if(G[i][j]){l=r+1;continue;}
					while(l<=r&&q[l]>j+mv.se) l++;
					while(l<=r&&f[p^1][i][q[r]]+q[r]<=f[p^1][i][j]+j) r--;
					q[++r]=j,f[p][i][j]=max(f[p][i][j],f[p^1][i][q[l]]+q[l]-j);
				}
			}
		} else if(mv.fi==4){ // 右-举的例子
			for(re int i=1;i<=n;i++){
				l=1,r=0;
				for(re int j=1;j<=m;j++){
					if(G[i][j]){l=r+1;continue;}
					while(l<=r&&q[l]<j-mv.se) l++;
					while(l<=r&&f[p^1][i][q[r]]-q[r]<=f[p^1][i][j]-j) r--;
					q[++r]=j,f[p][i][j]=max(f[p][i][j],f[p^1][i][q[l]]+j-q[l]);
				}
			}
		}
	}
	re int ans=-inf;
	for(re int i=1;i<=n;i++)
		for(re int j=1;j<=m;j++) ans=max(ans,f[p][i][j]);
	printf("%d\n",ans);
	return 0;
}

---

祝大家学习愉快！