Prim算法(三)之 Java详解

前面分别通过C和C++实现了普里姆，本文介绍普里姆的Java实现。

目录
1. 普里姆算法介绍
2. 普里姆算法图解
3. 普里姆算法的代码说明
4. 普里姆算法的源码

转载请注明出处：http://www.cnblogs.com/skywang12345/

更多内容：数据结构与算法系列 目录

普里姆算法介绍

普里姆(Prim)算法，是用来求加权连通图的最小生成树的算法。

基本思想
对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。
从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，直到U=V为止，最小生成树构造完毕，这时集合T中包含了最小生成树中的所有边。

普里姆算法图解

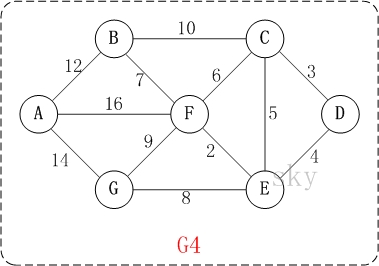
以上图G4为例，来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。

初始状态：V是所有顶点的集合，即V={A,B,C,D,E,F,G}；U和T都是空！
第1步：将顶点A加入到U中。
    此时，U={A}。
第2步：将顶点B加入到U中。
    上一步操作之后，U={A}, V-U={B,C,D,E,F,G}；因此，边(A,B)的权值最小。将顶点B添加到U中；此时，U={A,B}。
第3步：将顶点F加入到U中。
    上一步操作之后，U={A,B}, V-U={C,D,E,F,G}；因此，边(B,F)的权值最小。将顶点F添加到U中；此时，U={A,B,F}。
第4步：将顶点E加入到U中。
    上一步操作之后，U={A,B,F}, V-U={C,D,E,G}；因此，边(F,E)的权值最小。将顶点E添加到U中；此时，U={A,B,F,E}。
第5步：将顶点D加入到U中。
    上一步操作之后，U={A,B,F,E}, V-U={C,D,G}；因此，边(E,D)的权值最小。将顶点D添加到U中；此时，U={A,B,F,E,D}。
第6步：将顶点C加入到U中。
    上一步操作之后，U={A,B,F,E,D}, V-U={C,G}；因此，边(D,C)的权值最小。将顶点C添加到U中；此时，U={A,B,F,E,D,C}。
第7步：将顶点G加入到U中。
    上一步操作之后，U={A,B,F,E,D,C}, V-U={G}；因此，边(F,G)的权值最小。将顶点G添加到U中；此时，U=V。

此时，最小生成树构造完成！它包括的顶点依次是：A B F E D C G。

普里姆算法的代码说明

以"邻接矩阵"为例对普里姆算法进行说明，对于"邻接表"实现的图在后面会给出相应的源码。

1. 基本定义

public class MatrixUDG {

    private char[] mVexs;       // 顶点集合
    private int[][] mMatrix;    // 邻接矩阵
    private static final int INF = Integer.MAX_VALUE;   // 最大值

    ...
}

MatrixUDG是邻接矩阵对应的结构体。mVexs用于保存顶点，mEdgNum用于保存边数，mMatrix则是用于保存矩阵信息的二维数组。例如，mMatrix[i][j]=1，则表示"顶点i(即mVexs[i])"和"顶点j(即mVexs[j])"是邻接点；mMatrix[i][j]=0，则表示它们不是邻接点。

2. 普里姆算法

/*
 * prim最小生成树
 *
 * 参数说明：
 *   start -- 从图中的第start个元素开始，生成最小树
 */
public void prim(int start) {
    int num = mVexs.length;         // 顶点个数
    int index=0;                    // prim最小树的索引，即prims数组的索引
    char[] prims  = new char[num];  // prim最小树的结果数组
    int[] weights = new int[num];   // 顶点间边的权值

    // prim最小生成树中第一个数是"图中第start个顶点"，因为是从start开始的。
    prims[index++] = mVexs[start];

    // 初始化"顶点的权值数组"，
    // 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
    for (int i = 0; i < num; i++ )
        weights[i] = mMatrix[start][i];
    // 将第start个顶点的权值初始化为0。
    // 可以理解为"第start个顶点到它自身的距离为0"。
    weights[start] = 0;

    for (int i = 0; i < num; i++) {
        // 由于从start开始的，因此不需要再对第start个顶点进行处理。
        if(start == i)
            continue;

        int j = 0;
        int k = 0;
        int min = INF;
        // 在未被加入到最小生成树的顶点中，找出权值最小的顶点。
        while (j < num) {
            // 若weights[j]=0，意味着"第j个节点已经被排序过"(或者说已经加入了最小生成树中)。
            if (weights[j] != 0 && weights[j] < min) {
                min = weights[j];
                k = j;
            }
            j++;
        }

        // 经过上面的处理后，在未被加入到最小生成树的顶点中，权值最小的顶点是第k个顶点。
        // 将第k个顶点加入到最小生成树的结果数组中
        prims[index++] = mVexs[k];
        // 将"第k个顶点的权值"标记为0，意味着第k个顶点已经排序过了(或者说已经加入了最小树结果中)。
        weights[k] = 0;
        // 当第k个顶点被加入到最小生成树的结果数组中之后，更新其它顶点的权值。
        for (j = 0 ; j < num; j++) {
            // 当第j个节点没有被处理，并且需要更新时才被更新。
            if (weights[j] != 0 && mMatrix[k][j] < weights[j])
                weights[j] = mMatrix[k][j];
        }
    }

    // 计算最小生成树的权值
    int sum = 0;
    for (int i = 1; i < index; i++) {
        int min = INF;
        // 获取prims[i]在mMatrix中的位置
        int n = getPosition(prims[i]);
        // 在vexs[0...i]中，找出到j的权值最小的顶点。
        for (int j = 0; j < i; j++) {
            int m = getPosition(prims[j]);
            if (mMatrix[m][n]<min)
                min = mMatrix[m][n];
        }
        sum += min;
    }
    // 打印最小生成树
    System.out.printf("PRIM(%c)=%d: ", mVexs[start], sum);
    for (int i = 0; i < index; i++)
        System.out.printf("%c ", prims[i]);
    System.out.printf("\n");
}

普里姆算法的源码

这里分别给出"邻接矩阵图"和"邻接表图"的普里姆算法源码。

1. 邻接矩阵源码(MatrixUDG.java)

2. 邻接表源码(ListUDG.java)