OpenCascade Primitives BRep - Sphere

OpenCascade Primitives BRep - Sphere

eryar@163.com

Abstract. BRep is short for Boundary Representation. Boundary Representation gives a complete description of an object by associating topological and geometric information for solid modeling. In this case, objects are described by their boundaries. There are two types of information in BRep: Topological information and Geometric information. This paper is concerned with the sphere BRep in OpenCascade, and also show how to use Tcl script to dump sphere BRep info.

Key words. OpenCascade, BRep, Boundary Representation, Sphere, Singularity

1. Introduction

球体的几何数据主要是一个球面，在OpenCascade中球面的参数方程如下所示：

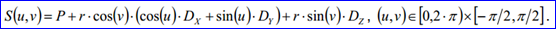
在《Parametric Curves and Surfaces》一文中，对参数曲线曲面进行了介绍，并重点介绍了球面的奇异性（Singularity）。本文通过对Sphere的BRep表示进行分析，来理解边界表示法中对参数曲面上奇点（Singular Point）的处理及BRep_TEdge中包含的多种形式的曲线。

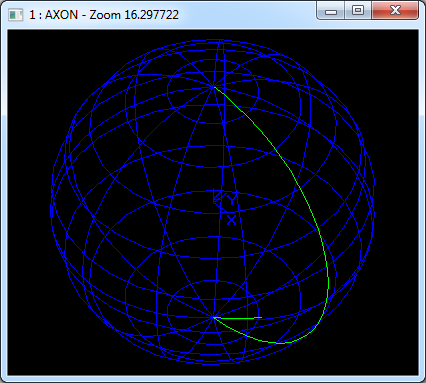
Figure 1.1 Sphere Generated by Tcl in Draw Test Harness

2. Dump Sphere BRep Info by Tcl

在OpenCascade中使用Tcl脚本来测试一些想法真是很方便，如这里要输出球的边界表示的数据，只需要三条命令就可以完成。以下Tcl命令生成了一个圆心在原点（0,0,0），半径为10的球：

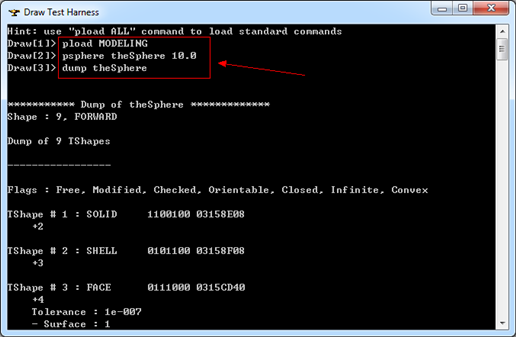
Figure 2.1 Dump Sphere BRep Info in Draw Test Harness

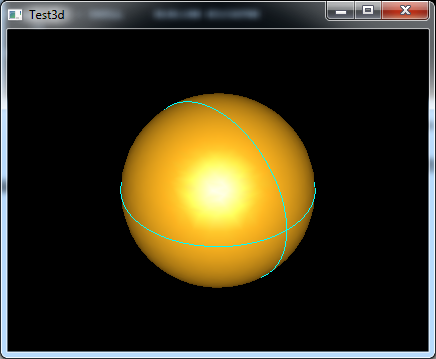
Figure 2.2 Display the Sphere in Draw

与《OpenCascade Primitives BRep - Box》一样，根据这些信息，从Vertex开始编号，来分析球的BRep表示。

3. Sphere BRep in OpenCascade

球的拓朴顶点Vertex有两个，分别是#7（0, 0, -10）和#9（0, 0, 10），如下图所示：

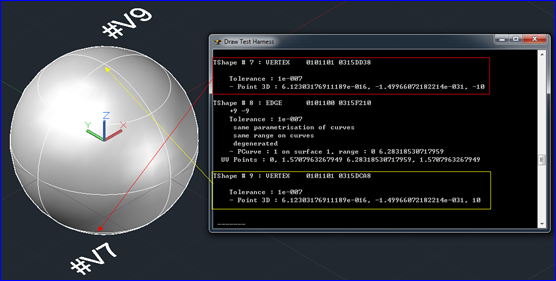
Figure 3.1 Vertex of Sphere BRep in OpenCascade

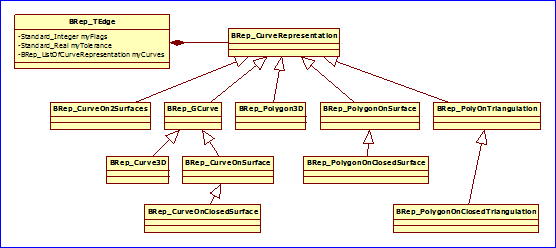
Figure 3.2 Curve Representation of BRep_TEdge

边Edge有三种表现形式，分别是#5，#6和#8，其中#5和#8是退化边（Degenerated Edge），即球面参数方程的奇点（Singular Point），在前文《PCurve - Curve on Surface》中分析曲面上曲线PCurve时已经讨论过，此处略过。本文只对#6边中的几何信息进行详细分析。

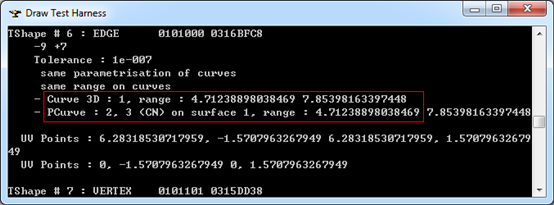
Figure 3.3 Edge #6 of Sphere BRep in OpenCascade

从拓朴边中可以看出#6Edge中的曲线有三个：一是三维空间曲线（Curve 3D）1；另外两个是曲面上曲线。其中三维空间曲线1的参数方程及其参数如下图所示：

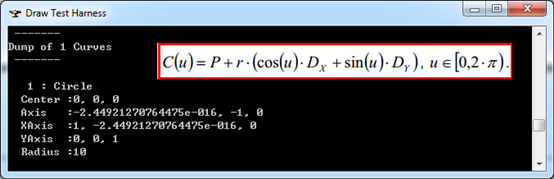
Figure 3.4 Parameters and Parametric equation of the Curve 3D

由上图可知，三维空间曲线1是一个圆，圆心位于坐标原点（0，0，0），半径为10，且位于XOZ平面上，对应范围的起点和终点分别为：

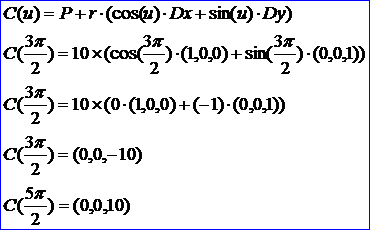
同理根据曲面上曲线的PCurve的定义，可以计算出曲面1上的曲线2和3，它们表示的曲线与三维空间曲线1相同，即边#6是衔接边（Seam Edge），对应OpenCascade中即是BRep_CurveOnClosedSurface。综上所述，可以画出球上的Edge，如下图所示：

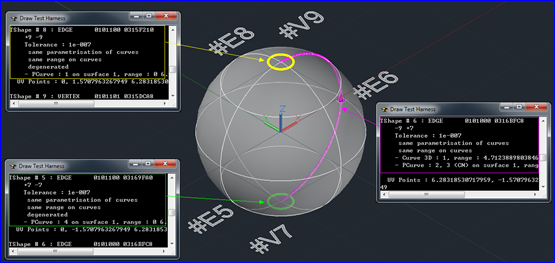
Figure 3.5 Edges of the Sphere

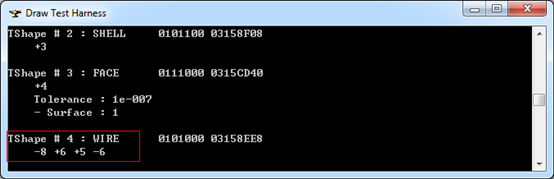
Figure 3.6 Wire of the Sphere

由上图可知在形成Wire时，Edge6使用了两次且方向相反，退化边（Degenerated Edge）的方向可忽略，因为其已经退化为一点。根据Wire的信息画出球的Wire如下图所示：

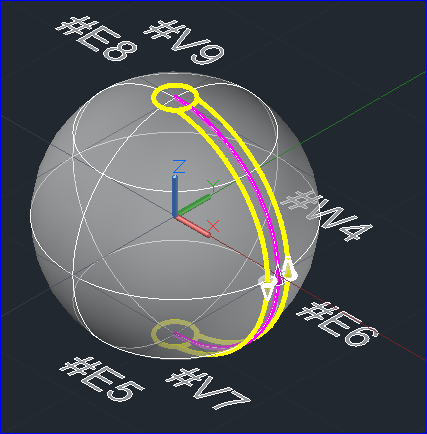
Figure 3.7 Wire of the Sphere(Wire in Yellow color)

由Wire#4组成了Face#3，Face#3中的几何曲面为1。曲面1是一个参数的球面。由Face#3组成Shell #2，由Shell#2组成了Solid#1。球的边界表示的分析就结束了。

4. Conclusion

本文通过使用Tcl脚本在Draw Test Harness中生成球的BRep边界表示信息，分析了球在OpenCascade中的组织方式。对BRep中边包含的多种几何曲线形式进行了解。

5. References

1. OpenCascade, Test Harness User’s Guide 2013

2. OpenCascade, BRep Format Description White Paper, 2013

3. John K. Ousterhout, Tcl and Tk Toolkit, 1993

PDF Version: OpenCascade Primitives BRep-Sphere