bzoj 5218: [Lydsy2017省队十连测]友好城市

题意：

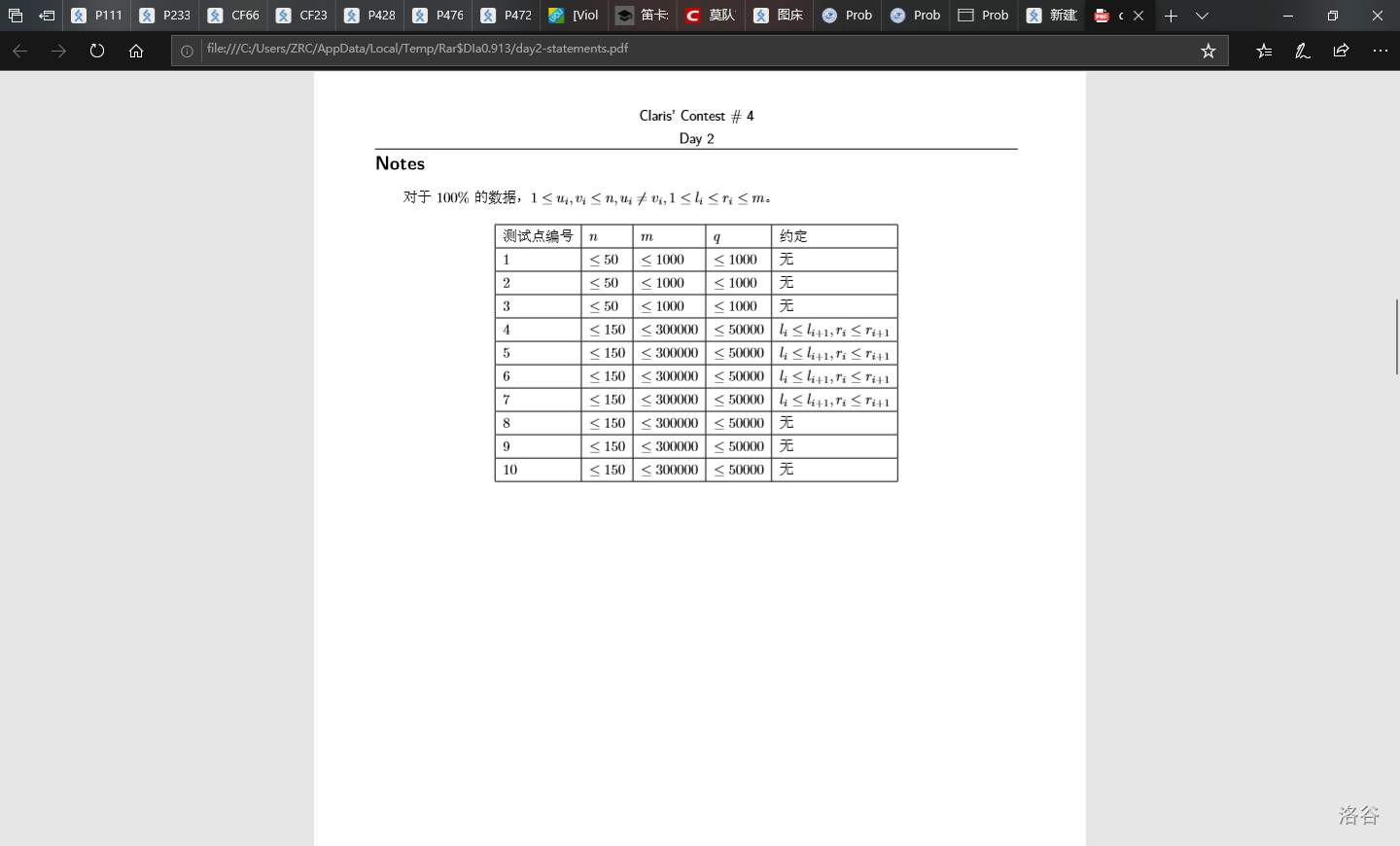
这题显然直接tarjan是做不了的。

这里安利另一个求SCC的算法Kosaraju，学习的话可以见这篇博客

于是结合莫队，我们有了个暴力。

发现主要瓶颈是dfs过程中找最小的未经过的点，我们用bitset优化一下就过了。

注意有重边，不能直接在biset中删除，要开个邻接矩阵判一下。

code:

#include<bits/stdc++.h>
using namespace std;
#define re register
typedef long long ll;
const int maxn=200;
const int maxm=3*1e5+10;
const int maxq=50010;
int n,m,Q,t,block,nowl=1,nowr,tot,cnt;
int pos[maxm],size[maxn],a[maxn];
int cnt1[maxn][maxn],cnt2[maxn][maxn];
ll ans[maxq];
struct Edge{int u,v;}E[maxm];
struct Query{int l,r,id;}qr[maxq];
bitset<maxn>vis;
bitset<maxn>e1[maxn],e2[maxn];
inline int read()
{
	re char c=getchar();re int res=0,f=1;
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')res=res*10+c-'0',c=getchar();
	return res*f;
}
char num[35];
inline void write(ll x)
{
    if(!x){putchar('0');return;}
	re ll tmp=x>0?x:-x;
    if(x<0)putchar('-');
    re int cnt=0;
    while(tmp>0)
	{
        num[cnt++]=tmp%10+'0';
        tmp/=10;
    }
    while(cnt>0)putchar(num[--cnt]);
}
inline bool cmp(Query x,Query y)
{
	if(pos[x.l]==pos[y.l])
	{
		if(pos[x.l]&1)return x.r<y.r;
		else return x.r>y.r;
	}
	else return x.l<y.l;
}
inline void add(int id)
{
	re int x=E[id].u,y=E[id].v;
	cnt1[x][y]++,cnt2[y][x]++;
	if(cnt1[x][y]==1)e1[x].set(y);
	if(cnt2[y][x]==1)e2[y].set(x);
}
inline void del(int id)
{
	re int x=E[id].u,y=E[id].v;
	cnt1[x][y]--,cnt2[y][x]--;
	if(!cnt1[x][y])e1[x].reset(y);
	if(!cnt2[y][x])e2[y].reset(x);
}
void dfs1(int x)
{
	vis.reset(x);
	bitset<maxn>now=vis&e1[x];
	while(now.any())
	{
		dfs1(now._Find_first());
		now&=vis;
	}
	a[++cnt]=x;
}
void dfs2(int x)
{
	size[tot]++;vis.reset(x);
	bitset<maxn>now=vis&e2[x];
	while(now.any())
	{
		dfs2(now._Find_first());
		now&=vis;
	}
}
inline ll solve()
{
	memset(size,0,sizeof(size));
	vis.set();cnt=tot=0;
	re ll res=0;
	for(re int i=1;i<=n;i++)if(vis.test(i))dfs1(i);
	vis.set();
	for(re int i=cnt;i;i--)if(vis.test(a[i]))tot++,dfs2(a[i]);
	for(re int i=1;i<=tot;i++)res+=size[i]*(size[i]-1)/2;
	return res;
}
int main()
{
	//freopen("test.in","r",stdin);
	//freopen("test.out","w",stdout);
	n=read(),m=read(),Q=read();
	for(re int i=1;i<=m;i++)E[i].u=read(),E[i].v=read();
	for(re int i=1;i<=Q;i++)qr[i].l=read(),qr[i].r=read(),qr[i].id=i;
	t=pow(m,1.0*3/5);
	for(re int i=1;i<=m;i++)pos[i]=(i-1)/t+1;
	sort(qr+1,qr+Q+1,cmp);
	for(re int i=1;i<=Q;i++)
	{
		while(nowl<qr[i].l)del(nowl++);
		while(nowl>qr[i].l)add(--nowl);
		while(nowr<qr[i].r)add(++nowr);
		while(nowr>qr[i].r)del(nowr--);
		ans[qr[i].id]=solve();
	}
	for(re int i=1;i<=Q;i++,puts(""))write(ans[i]);
	return 0;
}