编程范式 --- 函数式编程（Funtional Programming，简称FP）

• 函数式编程（Funtional Programming，简称FP）是一种编程范式，也就是如何编写程序的方法论

1. 主要思想：把计算过程尽量分解成一系列可复用函数的调用
2. 主要特征：函数是“第一等公民”：
   
   函数与其他数据类型一样的地位，可以赋值给其他变量，也可以作为函数参数、函数返回值

• 函数式编程最早出现在LISP语言，绝大大部分的代码编程语言也对函数式编程做了不同程度的支持，比如：Haskell、JavaScript、Python、Swift、Kotlin、Scala等
• 函数时编程中的几个常用的概念

1. Higher-Order Function、Function Currying
2. Functor、Applicatie Functor、Monad

• 参考资料：
  
  http://www.mokacoding.com/blog/functor-applicative-monads-in-pictures/

---

FP实践 - 传统写法

• 常规写法

// 假设要实现以下功能：[(num + 3) * 5 - 1] % 10 / 2
let num = 1
func add(_ v1: Int, _ v2: Int) -> Int { v1 + v2 }
func sub(_ v1: Int, _ v2: Int) -> Int { v1 - v2 }
func multiple(_ v1: Int, _ v2: Int) -> Int { v1 * v2 }
func divide(_ v1: Int, _ v2: Int) -> Int { v1 / v2 }
func mod(_ v1: Int, _ v2: Int) -> Int { v1 % v2 }
let result = divide(mod(sub(multiple(add(num, 3), 5), 1), 10), 2)
print(result) // 4

FP实践 - 函数式写法

• 柯里化

func add(_ v: Int) -> (Int) -> Int { { $0 + v } }
func sub(_ v: Int) -> (Int) -> Int { { $0 - v } }
func multiple(_ v: Int) -> (Int) -> Int { { $0 * v } }
func divide(_ v: Int) -> (Int) -> Int { { $0 / v } }
func mod(_ v: Int) -> (Int) -> Int { { $0 % v } }

• 函数合成

func composite(_ f1: @escaping (Int) -> Int,
               _ f2: @escaping (Int) -> Int) -> (Int) -> Int {
        return { f2(f1($0)) }
}
let fn = composite(add(3), multiple(5))
print(fn(num)) // 20

• 函数合成 - 利用符号

infix operator >>>: AdditoinPrecedence
func >>>(_ f1: @escaping (Int) -> Int,
         _ f2: @escaping (Int) -> Int) -> (Int) -> Int { return { f2(f1($0)) } }
let fn = add(3) >>> multiple(5)
print(fn(num)) // 20

 函数合成 - 利用符号 - 泛型
infix operator >>>: AdditoinPrecedence
func >>> <A, B, C>(_ f1: @escaping (A) -> B,
         _ f2: @escaping (B) -> C) -> (A) -> C { return { f2(f1($0)) } }
let fn = add(3) >>> multiple(5)
print(fn(num)) // 20

let fn = add(3) >>> multiple(5) >>> sub(1) >>> mod(10) >>> divide(2)
print(fn(num)) // 4

---

高阶函数（Higher-Order Function）

• 高阶函数是至少满足下列一个条件的函数：

1. 接受一个或多个函数作为输入（map、filter、reduce等）
2. 返回一个函数

• FP中到处都是高阶函数

柯里化（Currying）

• 将一个接受多参数的函数变换为一系列只接受单个参数的函数

func add1(_ v1: Int, _ v2: Int) -> Int { v1 + v2 }
add1(10, 20)
func add1(_ v: Int) -> (Int) -> Int { { $0 + v } }
add1(10)(20)

• Array、Optional的map方法接受的参数就是一个柯里化函数
• 三个参数柯里化

func add2(_ v1: Int, _ v2: Int, v3: Int) -> Int { v1 + v2 + v3 }
func add2(_ v3: Int) -> (Int) -> (Int) -> Int {
    // v2 == 20
    return { v2 in
        // v1 == 10
        return { v1 in
            return v1 + v2 + v3
        }
    }
}
add2(10, 20, 30)
add2(30)(20)(10)

• 两个参数柯里化 - 泛型

func currying<A, B, C>(_ fn: @escaping (A, B) -> C) -> (B) -> (A) -> C {
    return { b in
        return { a in
            return fn(a, b)
        }
    }
}
currying(add1(20)(10))

• 两个参数柯里化- 利用符号 - 泛型

prefix func ~<A, B, C>(_ fn: @escaping (A, B) -> C)
                         -> (B) -> (A) -> C {
    { b in { a in fn(a, b) } }
 }
 print((~sub(20)(10))  // -10
 // 合成函数-> 泛型柯里化
let fn = (~add)(3) >>> (~multiple)(5) >>> (~sub)(1) >>> (~mod)(10) >>> (~divide)(2)
print(fn(1)) // 4

• 三个参数柯里化 - 利用符号 - 泛型

prefix func ~<A, B, C, D>(_ fn: @escaping (A, B, C) -> D)
                            -> (C) -> (B) -> (A) -> D {
    { c in { b in { a in fn(a, b, c) } } }
}
print((~add2)(30)(20)(10)) // 60

函子（Functor）

• 像Array、Optional这样支持map运算的类型，成为函子（Functor）
• 怎么样的Type才能称之为函子呢？

func map<T>(_ fn: (Inner) -> T) -> Type<T>

• 数组和可选项是符合函子规定的公式：

func map<T>(_ fn: (Element) -> T) -> Array<T>   // [T]
func map<T>(_ fn: (Wrapped) -> T) -> Opional<T> // T?

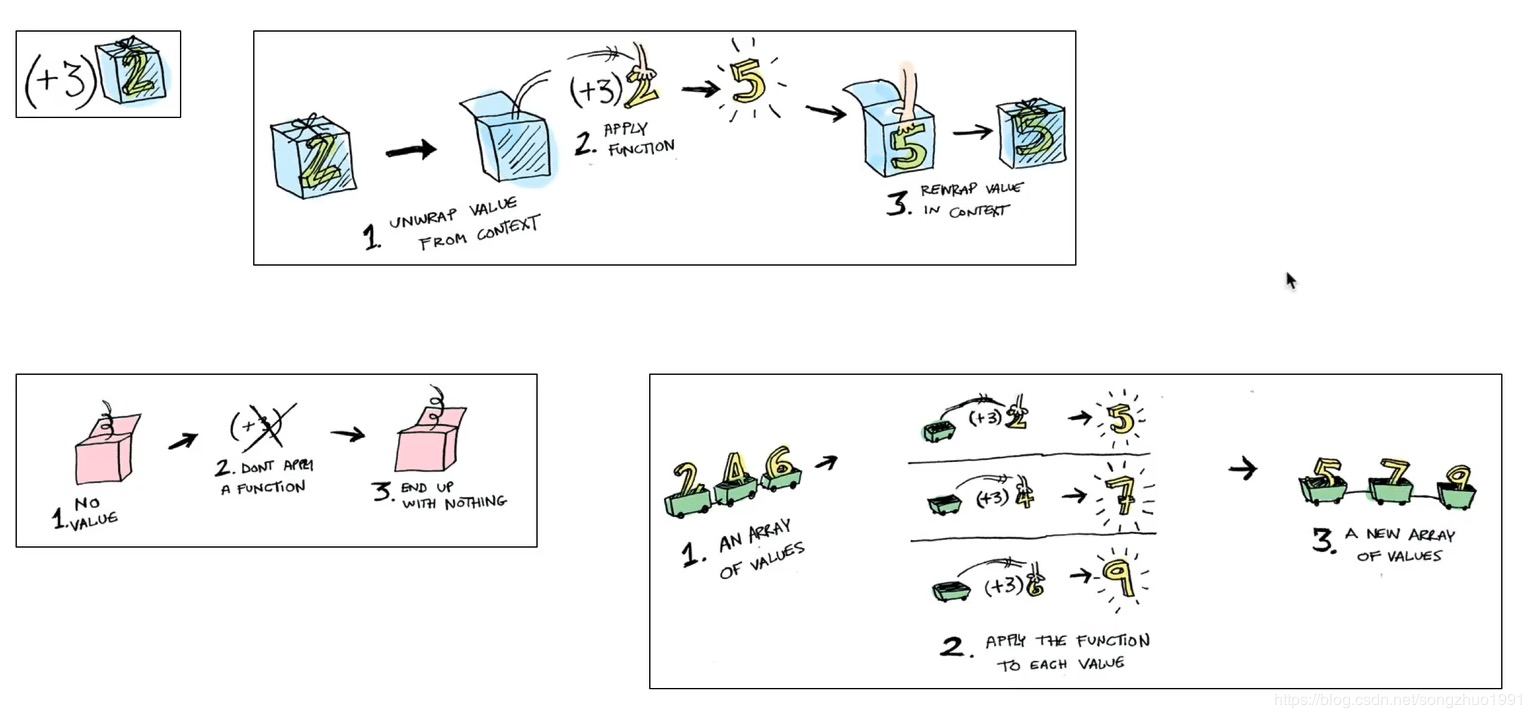
适用函子（Applicative Functor）

• 对任意一个函子F，如果能支持一下运算，该函子就是一个适用函子

func pure<A>(_ value: A) -> F<A>
func <*><A, B>(fn: F<(A) -> B>, value: F<A>) -> F<B>

• Optional可以成为适用函子

func pure<A>(_ value: A) -> A? { value }
infix operator <*>: AdditionPrecedence
func <*><A, B>(fn: ((A) -> B)?, value: A?) -> B? {
    guard let f = fn, let v = value else { return nil }
    return f(v)
}

var value: Int? = 10
var fn: ((Int) -> Int)? = { $0 * 2 }
// Optional
print(fn <*> value as Any)


• Array可以成为适用函子

func pure<A>(_ value: A) -> [A] { [value] }
func <*><A, B>(fn: [(A) -> B], value: [A]) -> [B] {
    var arr: [B] = []
    if fn.count == value.count {
        for i in fn.startIndex..<fn.endIndex {
            arr.append(fn[i](value[i]))
        }
    }
    return arr
}

// [10]
print(pure(10))
var arr = [{ $0 * 2 }, { $0 + 10 }, { $0 - 5 }] <*> [1, 2, 3]
// [2, 12, -2]
print(arr)

单子（Monad）

• 对于任意一个类型F，如果能支持一下运算，那么就可以成为是一个单子（Monad）

func pure<A>(_ value: A) -> F<A>
func flatMap<A, B>(_ value: F<A>, _ fn: (A) -> F<B>) -> F<B>

• 很显然，Array、Optional都是单子