DNA sequence（映射+BFS）

Problem Description

The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.

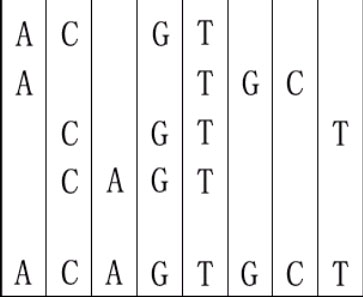
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

Input

The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.

Output

For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

SampleInput

1
4
ACGT
ATGC
CGTT
CAGT

SampleOutput

8

题意就是给你几个DNA序列，要求找到一个序列，使得所有序列都是它的子序列（不一定连续）。
直接搜MLE、TLE、RE，所以不能直接搜索，一般处理这种序列问题，都是把序列映射到整数或其他便于处理的东西上。
题目还说了每个DNA的序列长度不会超过5，所以我们可以按位处理映射到一个整数上，而且题目只需要我们输出最短的序列长度，所以我们也不必去映射字符，映射长度便够了。
最多8个字符，每个字符1-5长度，所以最大数为6^8。好为什么是6^8，不明明是5^8么，这个我暂时先不解释，我加在了代码注释里。
代码：

 #include <iostream>
 #include <string>
 #include <cstdio>
 #include <cstdlib>
 #include <sstream>
 #include <iomanip>
 #include <map>
 #include <stack>
 #include <deque>
 #include <queue>
 #include <vector>
 #include <set>
 #include <list>
 #include <cstring>
 #include <cctype>
 #include <algorithm>
 #include <iterator>
 #include <cmath>
 #include <bitset>
 #include <ctime>
 #include <fstream>
 #include <limits.h>
 #include <numeric>

 using namespace std;

 #define F first
 #define S second
 #define mian main
 #define ture true

 #define MAXN 1000000+5
 #define MOD 1000000007
 #define PI (acos(-1.0))
 #define EPS 1e-6
 #define MMT(s) memset(s, 0, sizeof s)
 typedef unsigned long long ull;
 typedef long long ll;
 typedef double db;
 typedef long double ldb;
 typedef stringstream sstm;
 const int INF = 0x3f3f3f3f;

 int t,n;
 map<int,int>vis;
 char s[][];    //保存序列
 int len[];    //保存每个序列的长度
 int p[] = {,,,,,,,,,};    //6的k次方表
 char temp[]={'A','C','G','T'};

 struct node{
     int step;    //长度
     int st;    //也就是映射数
     node(){}
     node(int _step, int _st):step(_step),st(_st){}
 };

 int bfs(int res){
     vis.clear();
     queue<node>q;
     q.push(node(,));
     vis[] = ;
     while(!q.empty()){
         node nxt,k = q.front();
         q.pop();
         if(k.st == res){    //当映射等于结果时 返回长度
             return k.step;
         }
         for(int i = ; i < ; i++){
             nxt.st = ;
             nxt.step = k.step+;
             int tp = k.st;
             for(int j = ; j <= n; j++){
                 int x = tp%;    //得到位数
                 tp /= ;
                 if(x == len[j] || s[j][x+] != temp[i]){    //判断字符是否匹配
                     nxt.st += x*p[j-];
                 }
                 else{
                     nxt.st += (x+)*p[j-];
                 }
             }
             if(vis[nxt.st] == ){    //标记是否已经搜过
                 q.push(nxt);
                 vis[nxt.st] = ;
             }
         }
     }
 }

 int main(){
     ios_base::sync_with_stdio(false);
     cout.tie();
     cin.tie();
     cin>>t;
     while(t--){
         cin>>n;
         int res = ;
         for(int i = ; i <= n; i++){    //因为数组从0开始计数，但我们映射以及后面操作都是基于位置，所以从1开始
             cin>>s[i]+;    //同理从一开始
             len[i] = strlen(s[i]+);
             res += len[i]*p[i-];    //这也就是为什么是6^8，因为我们是从1开始有5个状态而不是0
         }
         cout << bfs(res) <<endl;
     }
     return ;
 }

所以这题你非要从0位置搞，弄5^8确实没错，也可以做出来，但是操作会繁琐很多，还不如从方便的角度多加一个长度。

---

这道题的难度就是不知道怎么入手，即使知道转换处理也不知道该如何转换以及如何搜索，这里我们避免了去从字符开始搜索，而是直接基于长度搜。

值得一提的是，我问了队友后，他们表示这道题做法很多，还可以用IDA*算法或者启发式搜索，甚至不用搜索用AC自动机加矩阵也可以做。但这些做法都是基于字符去搜索的，也不能说谁好谁坏，只是我们的思维就不一样了，很多题目其实都不止一种解法，多想想，很有用的。至于其他做法我也就懒得做了（其实是不会23333）