快速傅里叶变换(FFT)学习笔记

定义

多项式

系数表示法

设\(A(x)\)表示一个\(n-1\)次多项式，则所有项的系数组成的\(n\)维向量\((a_0,a_1,a_2,\dots,a_{n-1})\)唯一确定了这个多项式。

即

\[A(x)=\sum \limits_{i=0}^{n-1}a_ix^i
\]

\[=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}
\]

点值表示法

将\(n\)个互不相同的\(x\)代入多项式，会得到\(n\)个互不相同的取值\(y\)。设他们组成的\(n\)维向量分别为\((x_0,x_1,x_2,\dots,x_{n-1}),(y_0,y_1,y_2,\dots,y_{n-1})\)。则给多项式被这两个\(n\)维向量唯一确定。

其中

\[y_i=A(x_i)=\sum \limits_{j=0}^{n-1}a_j\times x_i^j
\]

多项式乘法

定义两个多项式\(A(x)=\sum\limits_{i=0}^{n-1}a_ix^i\)与\(B(x)=\sum\limits_{i=0}^{n-1}b_ix^i\)相乘的结果为\(C(x)\)。

则

\(C(x)=A(x)\times B(x)=\sum\limits_{k=0}^{2n-2}(\sum \limits_{k=i+j} a_ib_j)x^k\)

形如\(C(k)=\sum \limits_{i\oplus j=k}a_ib_j\)的式子称为卷积，注意到，多项式乘法的本质就是加法卷积。

两个\(n-1\)次多项式相乘，得到的是一个\(2n-2\)次多项式，时间复杂度为\(O(n^2)\)。

若取两个多项式在\(2n-1\)个点处的点值表示，则

\[{y_3}_i=(\sum\limits_{j=0}^{2n-2}a_jx_i^j)\times(\sum\limits_{j=0}^{2n-2}b_jx_i^j)={y_1}_i\times{y_2}_i
\]

复数

设\(a,b\)为实数，\(i^2=-1\)，形如\(a+bi\)的数叫做复数，其中\(i\)被称为虚数单位。复数域是已知最大的域。

复平面

在复平面中，\(x\)轴代表实数，\(y\)轴代表虚数。每一个复数对应复平面上一个从\((0,0)\)指向\((a,b)\)的向量。

向量的长度\(\sqrt{a^2+b^2}\)叫做模长。表示从\(x\)轴正半轴到该向量的转角的有向角叫做幅角。

运算法则

记\(z_1=(a,b),z_2=(c,d)\)。

复数相加遵循平行四边形法则。\(z_1+z_2=(a+c,b+d)\)。

复数相乘时，模长相乘，幅角相加。\(z_1 \times z_2=(ac-bd,ad+bc)\)。

单位根

定义

下文中，默认\(n\)为2的正整数次幂。

在复平面上以原点为圆心，\(1\)为半径作圆，所得的圆叫单位圆。以原点为起点，圆的的\(n\)等分点为终点，作\(n\)个向量，设幅角为正且最小的向量对应的复数为\(\omega_n\)，则称\(\omega_n\)为\(n\)次单位根。

由复数的乘法定义（模长相乘，幅角相加）可知，其余的\(n-1\)个向量对应的复数分别为\(\omega_n^2,\omega_n^3,\dots,\omega_n^n\)，且易知\(\omega_n^0=\omega_n^n=1\)。

那么如何计算他们的值呢？

欧拉公式解决了这个问题：

\[\omega_n^k=\cos k\frac{2\pi}{n}+ i\sin k\frac{2\pi}{n}
\]

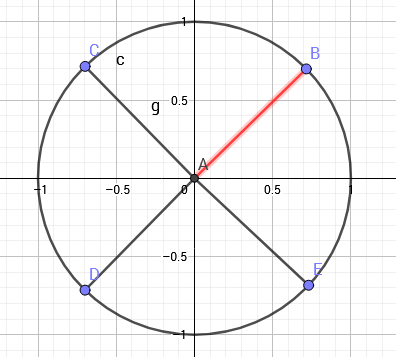
如图，向量\(\overrightarrow{AB}\)表示的复数为\(8\)次单位根，单位根的幅角为\(\frac{\pi}{n}\)

代数中，若\(z^n=1\)，则称\(z\)为\(n\)次单位根。

性质

• \(\omega_n^k=\cos k\frac{2\pi}{n}+ i\sin k\frac{2\pi}{n}\)

• \(\omega_{2n}^{2k}=\omega_n^k\)

从几何意义上来说，在复平面上，二者表示的向量终点相同。

证明：

\[\omega_{2n}^{2k}=\cos 2k \frac{2\pi}{2n}+i\sin 2k\frac{2\pi}{2n}=\cos k\frac{2\pi}{n}+ i\sin k\frac{2\pi}{n}=\omega_n^k
\]

• \(\omega_{n}^{k+\frac{n}{2}}=-\omega_n^k\)

证明：

\[\omega_n^{\frac{n}{2}}=\cos \frac{n}{2} \cdot \frac{2\pi}{n}+ i\sin \frac{n}{2} \cdot \frac{2\pi}{n}=\cos \pi+i\sin \pi=-1
\]

\[\omega_{n}^{k+\frac{n}{2}}=\omega_n^k\times\omega_n^{\frac{n}{2}}=-\omega_n^k
\]

• \(\omega_n^0=\omega_n^n=1\)

快速傅里叶变换(FFT)

前面提到过，一个\(n-1\)次多项式可以被\(n\)个点唯一确定。

考虑多项式\(A(x)\)的表示。将\(n\)次单位根的\(0\)到\(n-1\)次幂代入多项式的系数表示，所得点值向量\((A(\omega_n^0),A(\omega_n^1),\dots,A(\omega_n^{n-1}))\)称为其系数向量\((a_0,a_1,\dots,a_{n-1})\)的离散傅里叶变换。

但是按照朴素算法求离散傅里叶变换，时间复杂度仍然是\(O(n^2)\)。

\[A(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_{n-1}x^{n-1}
\]

考虑将多项式按照系数下标的奇偶分为两部分

\[A(x)=(a_0+a_2x^2+a_4x^4+\dots+a_{n-2}x^{n-2})+(a_1x+a_3x^3+a_5x^5+\dots+a_{n-1}x^{n-1})
\]

设

\[A_1(x)=a_0+a_2x+a_4x^2+\dots+a_{n-2}x^{\frac{n}{2}-1}
\]

\[A_2(x)=a_1+a_3x+a_5x^2+\dots+a_{n-1}x^{\frac{n}{2}-1}
\]

则有

\[A(x)=A_1(x^2)+xA_2(x^2)
\]

假设\(k<\frac{n}{2}\)，那么现在要求\(A(\omega_n^k)\)

\[A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})
\]

\[=A_1(\omega_{\frac{n}{2}}^{k})+\omega_n^kA_2(\omega_{\frac{n}{2}}^{k})
\]

对于\(A(\omega_n^{k+\frac{n}{2}})\)

\[A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}A_2(\omega_n^{2k+n})
\]

\[=A_1(\omega_n^{2k}\times\omega_n^n)-\omega_n^kA_2(\omega_n^{2k}\times\omega_n^n)
\]

\[=A_1(\omega_n^{2k})-\omega_n^kA_2(\omega_n^{2k})
\]

\[=A_1(\omega_{\frac{n}{2}}^{k})-\omega_n^kA_2(\omega_{\frac{n}{2}}^{k})
\]

神奇的事情发生了！注意到，当\(k\)取遍\([0,\frac{n}{2}-1]\)时，\(k\)和\(k+\frac{n}{2}\)取遍了\([0,n-1]\)。

这也就意味着，如果我们已经知道了\(A_1(x)\)和\(A_2(x)\)在\(\omega_{\frac{n}{2}}^0,\omega_{\frac{n}{2}}^1,\dots,\omega_{\frac{n}{2}}^{\frac{n}{2}-1}\)处的取值，那么我们就可以在\(O(n)\)的时间内求得\(A(x)\)在\(\omega_n^0,\omega_n^1,\dots,\omega_n^{n-1}\)处的取值。而关于\(A_1(x),A_2(x)\)的问题又都是相对原问题规模缩小了一半的子问题，所以只要不断的分治下去，而分治的边界就是一个常数项\(a_0\)。

该算法的时间复杂度为

\[T(n)=2T(n/2)+O(n)=O(n\log n)
\]

这就是最常用的\(FFT\)算法——\(Cooley-Tukey\)算法。

快速傅里叶逆变换(IFFT)

上面的讨论都是基于点值表示法的，但是在平时的应用中，很少用点值表示法来表示一个多项式。所以考虑将点值表示的多项式转化为系数表示，这个过程同样可以使用快速傅里叶变换，称为傅里叶逆变换。

设\((y_0,y_1,y_2,\dots,y_{n-1})\)为\((a_0,a_1,a_2,\dots,a_{n-1})\)的傅里叶变换（即点值表示），设有另一个向量\((c_0,c_1,c_2,\dots,c_{n-1})\)满足

\[c_k=\sum \limits_{i=0}^{n-1}y_i(\omega_n^{-k})^i
\]

即多项式\(B(x)=y_0+y_1x+y_2x^2+\dots+y_{n-1}x^{n-1}\)在\(\omega_n^0,\omega_n^{-1},\omega_n^{-2},\dots,\omega_n^{-(n-1)}\)处的点值表示。

下面就是推柿子时间，将上式展开，得到

\[c_k=\sum\limits_{i=0}^{n-1}y_i(\omega_n^{-k})^i
\]

\[=\sum\limits_{i=0}^{n-1}(\sum \limits_{j=0}^{n-1} a_j(\omega_n^i)^j)(\omega_n^{-k})^i
\]

\[=\sum\limits_{i=0}^{n-1}(\sum \limits_{j=0}^{n-1} a_j(\omega_n^j)^i)(\omega_n^{-k})^i
\]

\[=\sum\limits_{i=0}^{n-1}(\sum \limits_{j=0}^{n-1} a_j(\omega_n^j)^i(\omega_n^{-k})^i)
\]

\[=\sum\limits_{i=0}^{n-1}\sum \limits_{j=0}^{n-1} a_j(\omega_n^{j-k})^i
\]

\[=\sum \limits_{j=0}^{n-1} a_j(\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i)
\]

设\(S(x)=\sum \limits_{i=0}^{n-1}x^i\)

将\(\omega_n^k\)代入得

\(S(\omega_n^k)=1+\omega_n^k+(\omega_n^k)^2+\dots+(\omega_n^k)^{n-1}\)

当\(k\neq0\)时，两边同时乘上\(\omega_n^k\)，得

\(\omega_n^kS(\omega_n^k)=\omega_n^k+(\omega_n^k)^2+(\omega_n^k)^3+\dots+(\omega_n^k)^n\)

两边相减，整理后得到

\[\omega_n^kS(\omega_n^k)-S(\omega_n^k)=(\omega_n^k)^n-1
\]

\[S(\omega_n^k)=\frac{(\omega_n^k)^n-1}{\omega_n^k-1}
\]

分子为\(0\)，分母不为\(0\)，所以

\[S(\omega_n^k)=0
\]

当\(k=0\)时，显然\(S(\omega_n^k)=1\)

继续考虑上面的柿子

\[c_k=\sum \limits_{j=0}^{n-1} a_j(\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i)
\]

\[=\sum \limits_{j=0}^{n-1} a_jS(\omega_n^{j-k})
\]

当\(j=k\)时，\(S(\omega_n^{j-k})=n\)，否则\(S(\omega_n^{j-k})=0\)，即

\[c_i=na_i
\]

\[a_i=\frac{1}{n}c_i
\]

所以，使用单位根的倒数代替单位根，再做一次类似快速傅里叶变换的过程，最后将所得的每个数除以\(n\)，即为傅里叶逆变换的结果。

代码实现

递归实现

递归实现直接参照上面的结论来进行实现即可，比较直观。

需要注意的是，不要使用\(STL\)里的\(complex\)类，会被卡常数。

代码

#include <bits/stdc++.h>
using namespace std;

inline int ty() {
	char ch = getchar(); int x = 0, f = 1;
	while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
	return x * f;
}

const int _ = 4e6 + 10;
const double Pi = acos(-1.0);
struct Complex {
	double x, y;
	Complex(double _x = 0, double _y = 0) { x = _x, y = _y; }
	Complex operator+(const Complex &b) const { return Complex((double)x + b.x, (double)y + b.y); }
	Complex operator-(const Complex &b) const { return Complex((double)x - b.x, (double)y - b.y); }
	Complex operator*(const Complex &b) const { return Complex((double)x * b.x - (double)y * b.y, (double)x * b.y + (double)y * b.x); }
} a[_], b[_];
int N, M;

void fft(int lim, Complex *a, int op) {
	if (lim == 1) return;
	Complex a1[(lim >> 1) + 5], a2[(lim >> 1) + 5];
	for (int i = 0; i < lim; i += 2)
		a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
	fft(lim >> 1, a1, op);
	fft(lim >> 1, a2, op);
	Complex Wn = Complex(cos(2.0 * Pi / lim), op * sin(2.0 * Pi / lim)); // 单位根
	Complex w = Complex(1, 0);
	for (int i = 0; i < (lim >> 1); ++i, w = w * Wn) {
		a[i] = a1[i] + w * a2[i];
		a[i + (lim >> 1)] = a1[i] - w * a2[i];
	}
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("fft.in", "r", stdin);
	freopen("fft.out", "w", stdout);
#endif
	N = ty(), M = ty();
	for (int i = 0; i <= N; ++i) a[i].x = ty();
	for (int i = 0; i <= M; ++i) b[i].x = ty();
	int lim = 1; while (lim <= N + M) lim <<= 1;
	fft(lim, a, 1);
	fft(lim, b, 1);
	for (int i = 0; i <= lim; ++i) a[i] = a[i] * b[i];
	fft(lim, a, -1);
	for (int i = 0; i <= N + M; ++i) printf("%d ", (int)(a[i].x / lim + 0.5));
	return 0;
}

迭代实现

递归实现的\(FFT\)效率不高，实际当中一般用迭代实现。

二进制翻转

考虑递归 FFT 分治到边界时，每个数的顺序，及其二进制位。

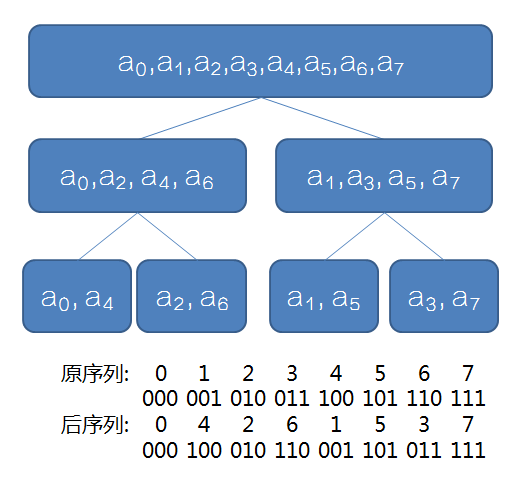
观察一下原序列和翻转后序列的联系，可以发现翻转后的序列下标其实就是原序列下标的二进制翻转。

因此对下标进行奇偶性分类其实是没有必要的，只需要\(O(n)\)求出翻转后的序列，然后不断进行向上合并即可。

蝴蝶操作

具体见代码。

代码

#include <bits/stdc++.h>
using namespace std;

inline int ty() {
	char ch = getchar(); int x = 0, f = 1;
	while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
	return x * f;
}

const int _ = 4e6 + 10;
const double Pi = acos(-1.0);
struct Complex {
	double x, y;
	Complex operator+(const Complex &b) const { return {x + b.x, y + b.y}; }
	Complex operator-(const Complex &b) const { return {x - b.x, y - b.y}; }
	Complex operator*(const Complex &b) const { return {x * b.x - y * b.y, x * b.y + y * b.x}; }
} a[_], b[_];
int N, M, pos[_];

void fft(const int lim, Complex *a, int op) {
	for (int i = 0; i < lim; ++i)
		if (i < pos[i]) swap(a[i], a[pos[i]]);
	for (int len = 2; len <= lim; len <<= 1) {
		int mid = len >> 1;
		Complex Wn = {cos(2.0 * Pi / len), op * sin(2.0 * Pi / len)};
		for (int i = 0; i < lim; i += len) {
			Complex w = {1, 0};
			for (int j = 0; j < mid; ++j, w = w * Wn) {
				Complex x = a[i + j], y = w * a[i + j + mid];
				a[i + j] = x + y;
				a[i + j + mid] = x - y;
			}
		}
	}
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("fft.in", "r", stdin);
	freopen("fft.out", "w", stdout);
#endif
	N = ty(), M = ty();
	for (int i = 0; i <= N; ++i) a[i].x = ty();
	for (int i = 0; i <= M; ++i) b[i].x = ty();
	int k = 0, lim = 1;
	while (lim <= N + M) lim <<= 1, ++k;
	for (int i = 0; i < lim; ++i) pos[i] = (pos[i >> 1] >> 1) | ((i & 1) << (k - 1));
	fft(lim, a, 1);
	fft(lim, b, 1);
	for (int i = 0; i <= lim; ++i) a[i] = a[i] * b[i];
	fft(lim, a, -1);
	for (int i = 0; i <= N + M; ++i) printf("%d ", (int)(a[i].x / lim + 0.5));
	return 0;
}

参考资料

FFT 学习笔记 | Menci's Blog

快速傅里叶变换(FFT)详解

[学习笔记&教程] 信号, 集合, 多项式, 以及各种卷积性变换 (FFT,NTT,FWT,FMT) - rvalue - 博客园

如何通俗地解释欧拉公式（e^πi+1=0）？

复数（数的概念扩展）_百度百科