【素数的判定-从暴力到高效】-C++

今天我们来谈一谈素数的判定。

对于每一个OIer来说，在漫长的练习过程中，素数不可能不在我们的眼中出现，那么判定素数也是每一个OIer应该掌握的操作，那么我们今天来分享几种从暴力到高效的判定方法。

---

1.直观判断法

因为这种方法其实就是我们平常所说的暴力法。根据素数的定义，不能被2~n-1之内的数整除的整数n就被称为素数。所以我们从2跑到n-1，每次取模判断即可，这是最直观的一种方法，代码如下：

bool isPrime_1(int num)
{
    int tmp=num-1;
    for(int i=2;i<=tmp;i++)
      if(num%i==0)
         return 0;
    return 1;
}

2.直观判断优化法

上述判断方法，明显存在效率极低的问题。对于每个数n，其实并不需要从2判断到n-1，我们知道，一个数若可以进行因数分解，那么分解时得到的两个数一定是一个小于等于sqrt(n)，一个大于等于sqrt(n)，据此，上述代码中并不需要遍历到n-1，遍历到sqrt(n)即可，因为若sqrt(n)左侧找不到约数，那么右侧也一定找不到约数！所以从2跑到sqrt（n）就可以了。代码如下：

bool isPrime_2(int num)
{
     int tmp=sqrt(num);
     for(int i=2;i<=tmp;i++)
        if(num%i==0)
          return 0;
     return 1;
}

3.另一种方法（没想名字）

这个方法我也忘记是在哪一篇博客上看到过的了，如果博主看到了联系我来补版权引用

首先看一个关于质数分布的规律：大于等于5的质数一定和6的倍数相邻。例如5和7，11和13,17和19等等；

证明：令x≥1，将大于等于5的自然数表示如下：

······ 6x-1，6x，6x+1，6x+2，6x+3，6x+4，6x+5，6(x+1），6(x+1)+1 ······

明显可以看到，不在6的倍数两侧，即6x两侧的数为6x+2，6x+3，6x+4，由于2(3x+1)，3(2x+1)，2(3x+2)，所以它们一定不是素数，再除去6x本身，显然，素数要出现只可能出现在6x的相邻两侧。这里要注意的一点是，在6的倍数相邻两侧并不一定就是质数。

此时判断质数可以以6为单位快进，即将方法（2）循环中i++步长加大为6，加快判断速度，原因是，假如要判定的数为n，则n必定是6x-1或6x+1的形式，对于循环中6i-1，6i，6i+1,6i+2，6i+3，6i+4，其中如果n能被6i，6i+2，6i+4整除，则n至少得是一个偶数，但是6x-1或6x+1的形式明显是一个奇数，故不成立；另外，如果n能被6i+3整除，则n至少能被3整除，但是6x能被3整除，故6x-1或6x+1（即n）不可能被3整除，故不成立。综上，循环中只需要考虑6i-1和6i+1的情况，即 循环的步长可以定为6，每次判断循环变量k和k+2的情况即可。

代码实现也很简单，不过需要注意的是有两种情况需要特判：

1.这个数是1，需要返回false;

2.这个数是2或3，需要返回true;

其他的按照上面的思路打出来就对了，代码如下：

bool isPrime_3(int num)
{
	 if(num==1)
		return 0;
     if(num==2||num==3)
        return 1;
     if(num%6!=1&&num%6!=5)
        return 0;
     int tmp=sqrt(num);
     for(int i=5;i<=tmp;i+=6)
        if(num%i==0||num%(i+2)==0)
           return 0;
     return 1;
}

接下来来测试一下用时；

注意：下面的用时是指从1~n分别判定是不是素数，不是判定一次！

那么就先把数据范围调到40W;

运行结果：



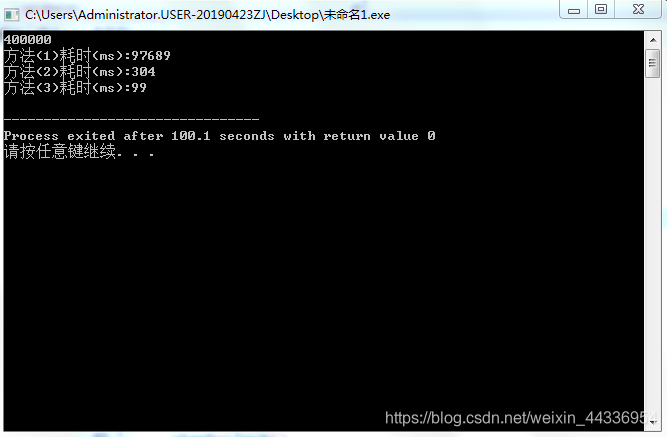
很明显，方法1实在太慢了！但是！虽然方法2已经很快速了，但耗时依然是方法3的三倍多！足以证明第三种方法的快速。

那接下来单独比较方法2和方法3，把n调到1000w试试、

运行结果：



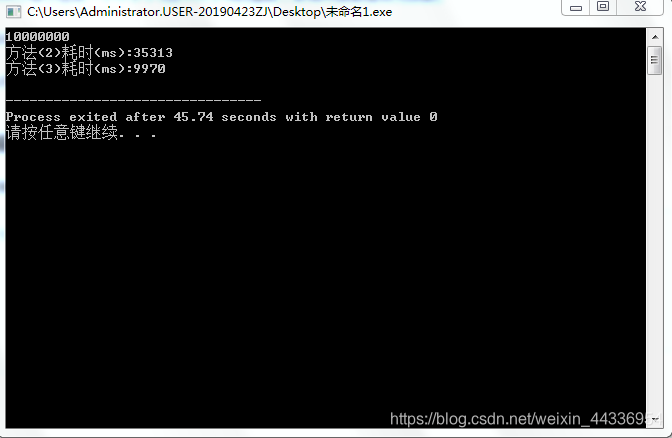
数据到了1000w的时候，方法3完全展示出了它的优势，这种用时在判定素数的方法中是非常节省用时得了。

看懂了上面的方法，分别用着去试一下过这道题目：

P3383 【模板】线性筛素数

ov.