面试中常见的算法之Java中的递归

1、方法定义中调用方法本身的现象
2、递归注意实现
1） 要有出口，否则就是死递归
2） 次数不能太多，否则就内存溢出
3） 构造方法不能递归使用
3、递归解决问题的思想和图解：

分解和合并【先分解后合并】

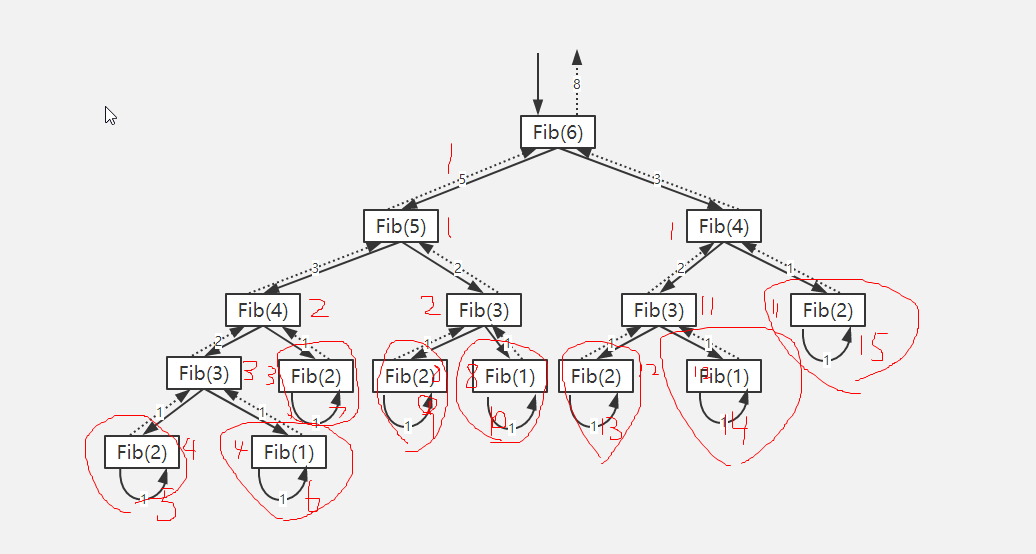
1. 常见的斐波那契数列

1，1，2，3，5，8，13，21，...
特征： 从第三个数开始，每个数是前两个数的和。

int count = 0;

    private int getFibo(int i) {

        if (i == 1 || i == 2) {
            count = count+1;
            System.out.println("第" +count+"次进行运算  并返回结果1" );
            return 1;}
        else
        {
            count = count+1;
            System.out.println("第" +count+"次进行运算  "+ "getFibo("+(i - 1)+")"+" + getFibo("+(i - 2)+")");
            return getFibo(i - 1) + getFibo(i - 2);
        }
    }

    @Test
    public void test01() {
       int value =  getFibo(6);
        System.out.println(value);
    }

　

　

2. 阶乘
10！= 10 * 9 * 8 * 7 * (... )* 1
9! = 9 * 8 * 7 * (... )* 1
8! = 8 * 7 * (... )* 1
特征：
9！=9* 8！
10！ =10 * 9!

//阶乘
    private int get(int i){
        int result = 1;
        if (i == 1) {
            count = count+1;
            System.out.println("第" +count+"次进行运算  并返回结果* 1" );
            result = result * 1;
        }
        else {
            count = count+1;
            System.out.println("第" +count+"次进行运算" + "get(" +(i-1)+")" );
            result = i * get(i-1);
        }
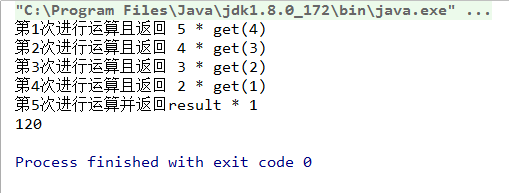
        return result;

    }

    @Test
    public void test01() {
        //System.out.println(getFibo(6));
        System.out.println(get(5));
    }

　　

3. 加法实现1+2+3+4+5+...+100=

 //求和
    private int fsum(int i){

        if (i <= 0) {
            count = count+1;
            System.out.println("第" +count+"次进行运算并返回0" );
            return 0;
        }
        else {
            count = count+1;
            System.out.println("第" +count+"次进行运算且返回 " + i +" + fsum(" +(i-1)+")" );
            return (i + fsum(i-1));

        }

    }

    @Test
    public void test01() {
        //System.out.println(getFibo(6));
        //System.out.println(get(5));
        System.out.println(fsum(10));

    }

　　

4. 实现打印乘法表

//打印乘法表
    //for 循环实现
    private void getByFor(int n) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                System.out.print(i+" * "+j+" = "+i*j+"  ");
            }
            System.out.println();
        }
    }
    //打印乘法表
    //递归实现
    public static void getByRecursion(int n) {//递归 实现
        if (n == 1) {
            System.out.println("1 * 1 = 1 ");
        }
        else {
            getByRecursion(n-1);
            for (int j = 1; j <= n; j++) {
                System.out.print(n+" * "+j+" = "+n*j+"  ");
            }
            System.out.println();
        }
    }

    @Test
    public void test01() {
        //System.out.println(getFibo(6));
        //System.out.println(get(5));
        //System.out.println(fsum(10));

        getByFor(8);
        getByRecursion(9);

    }

　　

6. 汉诺塔游戏

三根木棒，n个依次增大的空心圈圈，每次移动一个圈圈到木棒上，且任何时候保证小的圈圈不能被大的圈圈压在下面。

2的n次方-1

//5. 汉诺塔（又称河内塔）问题其实是印度的一个古老的传说
    public int hanio(int n,char a,char b,char c) {
        if (n == 1) {
            System.out.println( n + "号盘子从" + a + "到" + c);
            count = count+1;
            return count;

        } else {
            count = count+1;
            hanio(n - 1, a, c, b);//把上面n-1个盘子从a借助b搬到c
            System.out.println("移动" + n + "号盘子从" + a + "到" + c);//紧接着直接把n搬动c
            hanio(n - 1, b, a, c);//再把b上的n-1个盘子借助a搬到c
            return count;
        }

    }

    @Test
    public void test01() {
        //System.out.println(getFibo(6));
        //System.out.println(get(5));
        //System.out.println(fsum(10));

        //getByFor(8);
        //getByRecursion(9);

        int count =hanio(3,'A','B','C');
        System.out.println(count);

    }

　　

代码：

package com.example.demo;

import org.junit.Test;

public class Test02 {

    int count = 0;

    //1. 斐波那契数列递归，用的时候请将count和输出System.Out去除
    private int getFibo(int i) {

        if (i == 1 || i == 2) {
            count = count+1;
            System.out.println("第" +count+"次进行运算  并返回结果1" );
            return 1;}
        else
        {
            count = count+1;
            System.out.println("第" +count+"次进行运算  "+ "getFibo("+(i - 1)+")"+" + getFibo("+(i - 2)+")");
            return getFibo(i - 1) + getFibo(i - 2);
        }
    }

    //2. 阶乘
    private int get(int i){
        int result = 1;
        if (i == 1) {
            count = count+1;
            System.out.println("第" +count+"次进行运算并返回result * 1" );
            result = result * 1;
        }
        else {
            count = count+1;
            System.out.println("第" +count+"次进行运算且返回 " + i+" * get(" +(i-1)+")" );
            result = i * get(i-1);
        }
        return result;

    }

    //3. 求和
    private int fsum(int i){

        if (i <= 0) {
            count = count+1;
            System.out.println("第" +count+"次进行运算并返回0" );
            return 0;
        }
        else {
            count = count+1;
            System.out.println("第" +count+"次进行运算且返回 " + i +" + fsum(" +(i-1)+")" );
            return (i + fsum(i-1));

        }
    }

    //打印乘法表
    //for 循环实现
    private void getByFor(int n) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                System.out.print(i+" * "+j+" = "+i*j+"  ");
            }
            System.out.println();
        }
    }
    //打印乘法表
    //4. 递归实现
    public void getByRecursion(int n) {//递归 实现
        if (n == 1) {
            System.out.println("1 * 1 = 1 ");
        }
        else {
            getByRecursion(n-1);
            for (int j = 1; j <= n; j++) {
                System.out.print(n+" * "+j+" = "+n*j+"  ");
            }
            System.out.println();
        }
    }

    //5. 汉诺塔（又称河内塔）问题其实是印度的一个古老的传说
    public int hanio(int n,char a,char b,char c) {
        if (n == 1) {
            System.out.println( n + "号盘子从" + a + "到" + c);
            count = count+1;
            return count;

        } else {
            count = count+1;
            hanio(n - 1, a, c, b);//把上面n-1个盘子从a借助b搬到c
            System.out.println("移动" + n + "号盘子从" + a + "到" + c);//紧接着直接把n搬动c
            hanio(n - 1, b, a, c);//再把b上的n-1个盘子借助a搬到c
            return count;
        }

    }

    @Test
    public void test01() {
        //System.out.println(getFibo(6));
        //System.out.println(get(5));
        //System.out.println(fsum(10));

        //getByFor(8);
        //getByRecursion(9);

        int count =hanio(3,'A','B','C');
        System.out.println(count);

    }

}

　　

package com.example.demo;

import org.junit.Test;

public class Test03 {

    int count = 0;

    //1. 斐波那契数列递归，用的时候请将count和输出System.Out去除
    private int getFibo(int i) {

        if (i == 1 || i == 2) {
            return 1;}
        else
        {
           return getFibo(i - 1) + getFibo(i - 2);
        }
    }

    //2. 阶乘
    private int get(int i){
        int result = 1;
        if (i == 1) {
            result = result * 1;
        }
        else {
            result = i * get(i-1);
        }
        return result;

    }

    //3. 求和
    private int fsum(int i){

        if (i <= 0) {
            return 0;
        }
        else {
           return (i + fsum(i-1));

        }
    }

    //打印乘法表
    //for 循环实现
    private void getByFor(int n) {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                System.out.print(i+" * "+j+" = "+i*j+"  ");
            }
            System.out.println();
        }
    }
    //打印乘法表
    //4. 递归实现
    public void getByRecursion(int n) {//递归 实现
        if (n == 1) {
            System.out.println("1 * 1 = 1 ");
        }
        else {
            getByRecursion(n-1);
            for (int j = 1; j <= n; j++) {
                System.out.print(n+" * "+j+" = "+n*j+"  ");
            }
            System.out.println();
        }
    }

    //5. 汉诺塔（又称河内塔）问题其实是印度的一个古老的传说
    public int hanio(int n,char a,char b,char c) {
        if (n == 1) {
            System.out.println( n + "号盘子从" + a + "到" + c);
            count = count+1;
            return count;

        } else {
            count = count+1;
            hanio(n - 1, a, c, b);//把上面n-1个盘子从a借助b搬到c
            System.out.println("移动" + n + "号盘子从" + a + "到" + c);//紧接着直接把n搬动c
            hanio(n - 1, b, a, c);//再把b上的n-1个盘子借助a搬到c
            return count;
        }

    }

    @Test
    public void test01() {
        System.out.println(getFibo(6));
        System.out.println(get(5));
        System.out.println(fsum(10));

        getByFor(8);
        getByRecursion(8);

        int count =hanio(3,'A','B','C');
        System.out.println(count);

    }

}