RMQ(区间最值问题)

问题：

　　RMQ (Range Minimum/Maximum Query)问题是指：对于长度为n的数列A，回答若干询问RMQ(A,i,j)(i,j<=n)，返回数列A中下标在i,j里的最小(大）值，也就是说，RMQ问题是指求区间最值的问题。

dp思想：

　　dp[i][j]中存储的是从第i个数开始的2^j个数最大的数。（如下图）

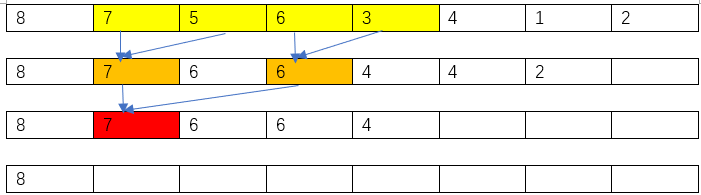
　　dp[2][2]表示的是2到2+2²-1中最大的数。即下表2-5中最大的数。

　　如果要求2-7中最大的数，可以先将区间拆成两个2^x长度的字串，分别求字串的最大值。2-7可以拆分成2-5和4-7这两个序列长度都为4.所以直接比较dp[2][2]和dp[4][2]即可。

dp代码：

const int maxn=1e5+;
int dp[maxn][];
int vis[maxn];

//处理dp数组
void rmq(int n,int a[]){
    vis[]=-;
    for(int i=;i<n;i++){
        vis[i]=((i&(i-))==)?vis[i-]+:vis[i-];//标记0.0
        dp[i][]=a[i];
    }
    for(int j=;j<=vis[n];j++){
        for(int i=;i+(<<j)-<=n;i++){
            dp[i][j]=max(dp[i][j-],dp[i+(<<(j-))][j-]);
        }
    }
}
//查询最大值
int rmpp(int x,int y){
    int k=vis[y-x+];
    return max(dp[x][k],dp[y-(<<k)+][k]);
}

补充：

　　上述代码有一个标记，代表此行代码和如下代码功能相同。

int ans=;
vis[]=-;
for(int i=;i<n;i++){
    if(i==ans){
        ans*=;
        vis[i]=vis[i-]+;
    }
    else vis[i]=vis[i];
}

n&（n-1）可以判断一个数是不是2的整数次幂