逆元 组合A(n,m) C(n,m)递推 隔板法

求逆元 https://blog.csdn.net/baidu_35643793/article/details/75268911

int inv[N];

void init(){
    inv[] = ;
    for (int i = ; i < N; ++ i){
        inv[i] = (mod - 1ll * (mod / i) * inv[mod % i] % mod) % mod;
    }
}

组合递推

牛客暑期集训第六场C题解

对于A，M个取i个排列，如果我们要使A(M,i)->A(M,i+1)只需要A(M,i) * (M-i)

对于C，N个取i个组合，如果我们要使C(N-1,i-1)->C(N-1,i)只需要

　　　　C(N-1,i-1) * (N-i)/i = C(N-1,i-1) * (N-i)*inv[i]%mod

#include <bits/stdc++.h>
#define MOD 998244353
#define MAXN 1000005
#define ll long long
using namespace std;

int NY[MAXN];
void init() {
    NY[]=;
    for(int i=;i<MAXN;i++)
        NY[i]=(MOD-1ll*(MOD/i)*NY[MOD%i]%MOD)%MOD;
}

int main()
{
    init();
    int t; scanf("%d",&t);
    for(int o=;o<=t;o++) {
        ll n,m; scanf("%lld%lld",&n,&m);
        ll A=m%MOD, C=;
        ll ans=1ll*A%MOD;
        for(ll i=;i<min(n,m);i++) {
            A=1ll*(m-i)%MOD*A%MOD;
            C=1ll*(n-i)%MOD*C%MOD*NY[i]%MOD;// C*((n-1)-(i-1))*NY[i]
            ans=(ans+A*C%MOD)%MOD;
        }
        printf("Case #%d: %lld\n",o,ans);
    }

    return ;
}

需要取模的组合数 预处理出所有

直接调用 C(a,b) 即可

#define mod 1000000007
#define LL long long
const int N=2e5+;
LL pow_mod(LL a, LL b) {
    LL res = 1LL; a %= mod;
    while(b){
        if(b & ) res = res * a % mod;
        a = a * a % mod;
        b >>= ;
    } return res;
}
LL inv(LL a) { return pow_mod(a, mod-); }
LL F[N], Finv[N];//F是阶乘，Finv是逆元的阶乘
void init() {
    F[] = Finv[] = 1LL;
    for(int i = ; i < N; i ++){
        F[i] = F[i-] * 1LL * (LL)i % mod;
        Finv[i] = Finv[i-] * 1LL * inv(i) % mod;
    }
}
LL C(LL n, LL m) {
    if(m <  || m > n) return ;
    return F[n] * 1LL * Finv[n - m] % mod * Finv[m] % mod;
}

隔板法 https://zhidao.baidu.com/question/1113648010040924539.html

隔板法就是把n个相同单元分配成m组。

这样n个单元中间有n-1个空格，分成m组需要m-1块隔板，

当必须分成m组 即各组不为空时，就是C（n-1，m-1）种方法

当至多分为m组 即有些组为空时，就是C（m+n-1，n-1）种方法

注意：隔板法的单元必须是相同的。

组合数的各种性质和定理

https://blog.csdn.net/litble/article/details/75913032

1.

2.   

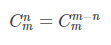
3.

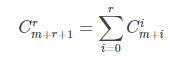
4.

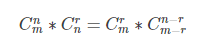
5.

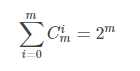
6.

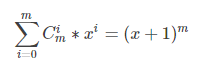
7.

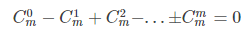
8.

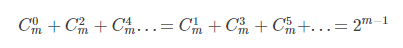
9.

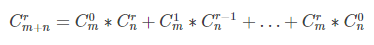
10.

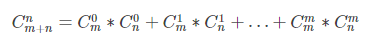
11.

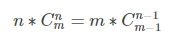
12.

13.

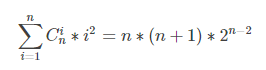
14.

15.