@总结 - 12@ burnside引理与pólya定理

@0 - 参考资料@
@1 - 问题引入@
@2 - burnside引理@
@3 - pólya定理@
@4 - pólya定理的生成函数形式@

@0 - 参考资料@

@1 - 问题引入@

一个经典问题：

一正方形分成4格，2着色，有多少种方案？
其中，经过转动相同的图象算同一方案。

假如不考虑转动，各种方案如下所示。

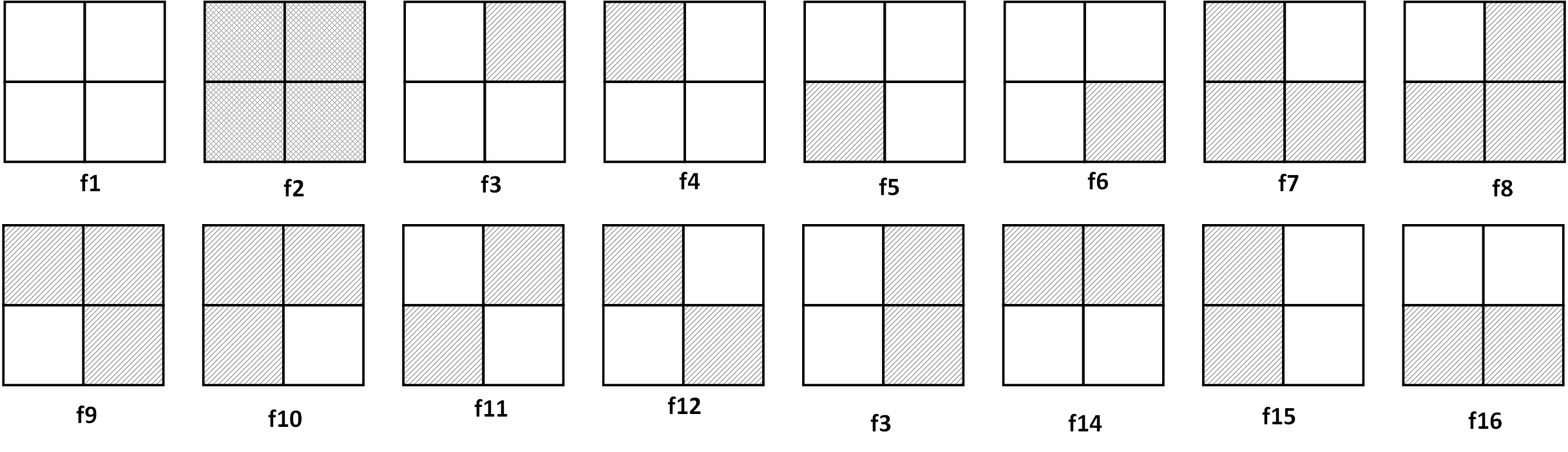
首先可以发现，转动的角度只有 4 种：0°，90°，180°，270°。
然后可以得到，每一次转动可以将一个方案唯一映射成另一个方案（可以是自身）。
于是我们可以用一个置换 p 描述一次旋转的效果，其中 p[i] 表示第 i 种方案被映射成了第 p[i] 种方案。

在这个例子中，4 种置换（0°，90°，180°，270°）构成了一个置换群。
（什么是置换群。。。emmm可以自行左转百度）

（以下的记法都是不严谨的，因为是根据我自己的记忆写的）
如果置换 f 使得元素 i 映射成 j，我们就记作 $f:i -> j$。

对于置换群 G，如果存在 $f\in G$，以及 $f:x -> y$，我们就称 x, y 为等价类。
显然这个等价关系满足传递性、自反性、对称性（对应群的几个性质）。
那么我们相等于求在置换群G的作用下的等价类个数。

@2 - burnside引理@

先抛结论：

我们称对于 f，满足 f:x -> x 的 x 为 f 作用下的不动点。记 c(f) 表示 f 的不动点个数。
则 G 作用下的等价类个数为：
\[cnt = \frac{\sum_{f\in G}c(f)}{|G|}\]

证明是我自己BB的，与主流证法不大一样（我也记不到主流证法了），所以可能不够简便。

引入（一个非常不严谨的）记法：记 $S_{i, j}$ 表示将 i 映射到 j 的置换组成的集合。

首先证明几个引理：

引理 1：$|S_{i, j}| = |S_{j, i}|$
证明：等价于证明 $|S_{i, j}| \le |S_{j, i}|$ 且 $|S_{j, i}| \le |S_{i, j}|$。
只需考虑 $|S_{i, j}| \le |S_{j, i}|$，另一半同理可证。
对于 $f \in S_{i, j}$，它的逆元 $f^{-1} \in S_{j, i}$。且根据置换群的性质，每个元素的逆元是唯一的，且不同元素的逆元不同。
所以 $S_{j, i}$ 至少含有 $|S_{i, j}|$ 个元素——即它们的逆元。

引理 2：若 $S_{i, j}$ 不为空，则 $|S_{i, j}| = |S_{i, i}|$
证明：只需证明 $|S_{i, j}| \le |S_{i, i}|$ 且 $|S_{i, i}| \le |S_{i, j}|$。
从 $S_{j, i}$ 中任选一个元素 $f$，$f$ 与 $S_{i, j}$ 中的每一个 $g$ 相乘得到 $f*g$。
显然有 $f*g \in S_{i, i}$，且 g 不相同时，得到的结果也一定不同，所以 $|S_{i, j}| \le |S_{i, i}|$。
然后依然是从 $S_{j, i}$ 中任选一个元素 $f$，$f$ 与 $S_{i, i}$ 中的每一个 $g$ 相乘得到 $f*g$。
有 $f*g \in S_{j, i}$，且 g 不相同时，得到的结果也不同。故又得到 $|S_{i, i}| \le |S_{j, i}| = |S_{i, j}|$（由引理 1）。

引理 3：一个等价类中的不动点数量总和 = |G|。
证明：设该等价类 $E = {x_1, x_2, ..., x_k}$。
则有 $\sum_{i=1}^{k}|S_{x_1, x_i}| = |G|$（每个在 G 中的置换一定会把 $x_1$ 映射成等价类中的某个数）。
根据引理 1 + 引理 2，可以得到 $\sum_{i=1}^{k}|S_{x_i, x_i}| = |G|$，于是得证。

有了引理 3，就可以推导出我们的 burnside 引理的正确性了，因为不动点的总数 = 等价类个数*|G|。

@3 - pólya定理@

（注意是 pólya 定理而不是 polya 定理，虽然这不重要不过还是要看起来专业点）

burnside 引理提出了一种统计等价类的一般方法，而 pólya 定理提出了在染色问题下的不动点具体计算方法。

在我们一开始给出的问题中，假如我们要老老实实地算，要算 2^(2+2) 个方案在置换下是否为不动点。
当数据范围增大时，方案数急剧增大，burnside引理就失去了意义。

我们不妨把 2*2 个点拿出来，构建置换群。以下假设可用颜色数量为 m。

我们将每个置换循环分解，则这个置换作用下的不动点肯定是相同循环内的元素涂相同颜色。
设置换 f 的循环分解后共有 c(f) 个循环，则 f 作用下不动点数量为 $m^{c(f)}$。

则 G 作用下不动点数量为：
\[cnt = \frac{\sum_{f\in G}m^{c(f)}}{|G|}\]

这样就可以将指数级复杂度化为多项式复杂度。

@4 - pólya定理的生成函数形式@

~~可以发现，pólya 定理是非常显然的。~~但同时 pólya 定理也是非常普遍应用的。

但是！如果结合万能的生成函数，我们就可以得到一些更有趣的东西。

还是一开始的典型例子，假如我们想要知道固定黑色格子有多少个时，本质不同的方案数。
这时候我们就需要利用生成函数了。

假如置换 f 进行循环分解得到 k 个循环，每个循环的循环节大小分别为 x1, x2, ..., xk。
则这个置换 f 对应的生成函数为 $F(f) = \prod_{i=1}^{k}(b^{x_i} + w^{x_i})$。其中 b, w 就是形式变量。
整个置换群 G 的生成函数为：
\[F(G) = \frac{\sum_{f\in G}F(f)}{|G|}\]

则 G 中的 $b^i*w^j$ 项的系数等于涂 i 格黑色与 j 格白色的方案数。
比如对于我们一开始的例子，生成函数为：
\[F(G) = \frac{1}{4}((b + w)^4 + (b^4 + w^4) + (b^2 + w^2)^2 + (b^4 + w^4)) = w^4+w^3b+2w^2b^2+wb^3+b^4\]

验证一下就可以发现它的正确性。