数字三角形 · Triangle

从上到下用DP。

［抄题］：

给定一个数字三角形，找到从顶部到底部的最小路径和。每一步可以移动到下面一行的相邻数字上。

比如，给出下列数字三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

从顶到底部的最小路径和为11 ( 2 + 3 + 5 + 1 = 11)。

［思维问题］：

不知道要初始化，把距离定义好。

［一句话思路］：　　

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

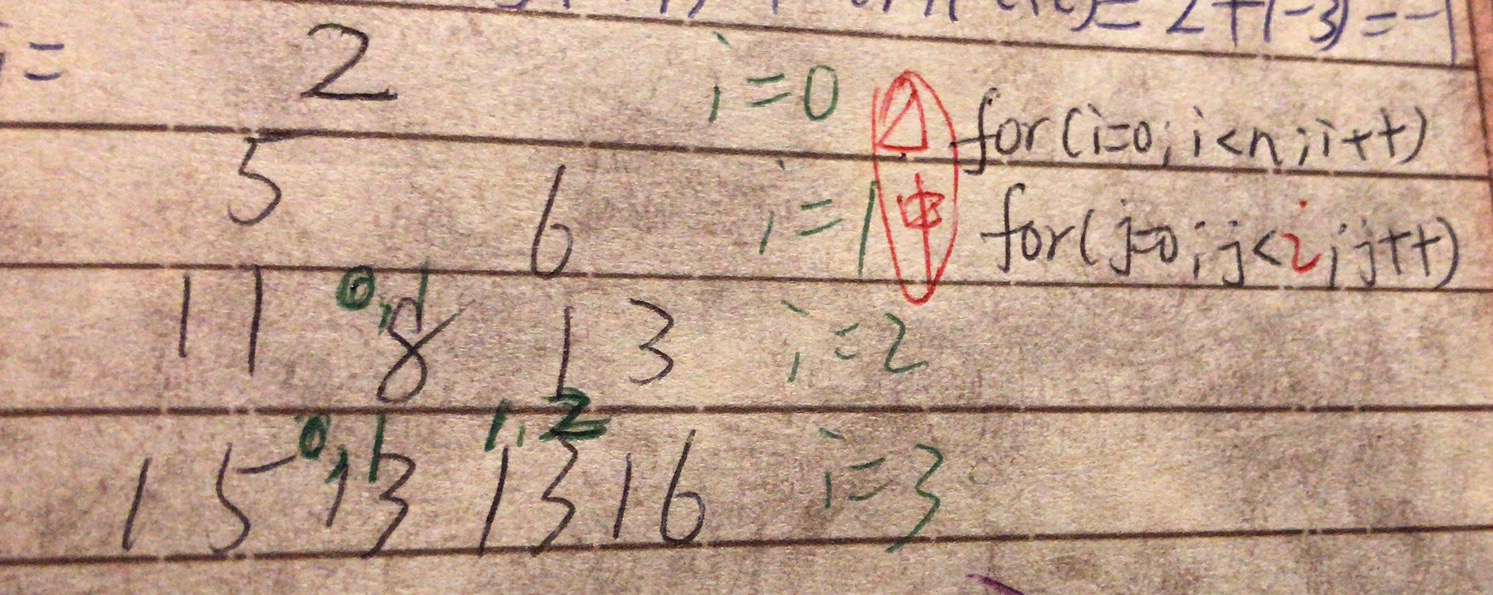
［一刷］：

1. 定义原点后，top-down和比较best的i j 都从1开始

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

1. 忘记初始化[0][0]了

［总结］：

按步骤写，注意条件：取过[0][0]后，循环都从1开始

［复杂度］：几个点*每个点被看几次*被看时的处理

Time complexity: O(n^2) Space complexity: O(n^2)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

1. 和树的区别：有多条路径到达叶子节点。树由于父子关系，只有一条路径。
2. 搜索的本质：用递归找出所有方法 虽然看不到结果。（枚举能看到结果）

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

public class Solution {
    /**
     * @param triangle: a list of lists of integers.
     * @return: An integer, minimum path sum.
     */
    public int minimumTotal(int[][] triangle) {
        if (triangle == null || triangle.length == 0) {
            return -1;
        }
        if (triangle[0] == null || triangle[0].length == 0) {
            return -1;
        }

        // state: f[x][y] = minimum path value from 0,0 to x,y
        int n = triangle.length;
        int[][] f = new int[n][n];

        // initialize
        f[0][0] = triangle[0][0];
        for (int i = 1; i < n; i++) {
            f[i][0] = f[i - 1][0] + triangle[i][0];
            f[i][i] = f[i - 1][i - 1] + triangle[i][i];
        }

        // top down
        for (int i = 1; i < n; i++) {
            for (int j = 1; j < i; j++) {
                f[i][j] = Math.min(f[i - 1][j], f[i - 1][j - 1]) + triangle[i][j];
            }
        }

        // answer
        int best = f[n - 1][0];
        for (int i = 1; i < n; i++) {
            best = Math.min(best, f[n - 1][i]);
        }
        return best;
    }
}

记忆化搜索

［抄题］：

［思维问题］：

不知道为什么要存MAX_VALUE: 为了产生一个可以被记忆的最小值，把每个结果都和MAX_VALUE比较一下。

［一句话思路］：

1. 利用recursion，在search方法中把每次search的结果都用变量保存下来
2. minSum[i][j]的初始化应该在主函数中

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

［一刷］：

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

记忆化搜索的本质是递归recursion

［复杂度］：Time complexity: O() Space complexity: O()

［英文数据结构或算法，为什么不用别的数据结构或算法］：

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：

1. 成员变量与方法内部的变量重名时，希望在方法内部调用成员变量，这时候只能使用this

public class Solution {
    private int n;
    private int[][] minSum;
    private int[][] triangle;

    private int search(int x, int y) {
        if (x >= n) {
            return 0;
        }

        if (minSum[x][y] != Integer.MAX_VALUE) {
            return minSum[x][y];
        }

        minSum[x][y] = Math.min(search(x + 1, y), search(x + 1, y + 1))
            + triangle[x][y];
        return minSum[x][y];
    }

    public int minimumTotal(int[][] triangle) {
        if (triangle == null || triangle.length == 0) {
            return -1;
        }
        if (triangle[0] == null || triangle[0].length == 0) {
            return -1;
        }

        this.n = triangle.length;
        this.triangle = triangle;
        this.minSum = new int[n][n];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                minSum[i][j] = Integer.MAX_VALUE;
            }
        }

        return search(0, 0);
    }
}