本质矩阵E求解及运动状态恢复
为了获取本质矩阵,首先计算基础矩阵F。根据本质矩阵E,即可恢复得到运动的状态R和T。
由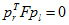 可以根据匹配点得到F,然后根据
可以根据匹配点得到F,然后根据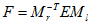 和相机内参,即可得到本质矩阵E。进而根据:
和相机内参,即可得到本质矩阵E。进而根据:
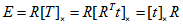

注意:根据摄像机模型t=-RT,恢复运动状态,就是要计算t和R。
8点法
8点算法是计算基本矩阵的最简单的方法,它涉及构造并(最小二乘)解一个线性方程组。给定足够多的匹配点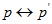 (至少7对),可解得基础矩阵F。
(至少7对),可解得基础矩阵F。
记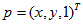 和
和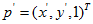 ,每一组点匹配提供关于
,每一组点匹配提供关于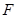 的未知元素的一个线性方程。对应于一对点
的未知元素的一个线性方程。对应于一对点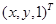 和
和 的方程是:
的方程是:
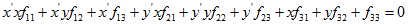
写成矩阵(矢量)的形式:
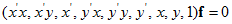
其中:
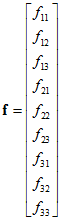
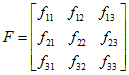
从而根据n对匹配的点集,我们可以得到线性方程组:
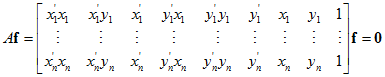
计算最小二乘解,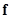 的最小二乘解是对应于
的最小二乘解是对应于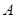 的最小奇异矩阵的奇异矢量,即是
的最小奇异矩阵的奇异矢量,即是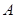 的SVD分解
的SVD分解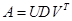 中矩阵
中矩阵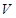 的最后一列矢量。用这种方法得到的解矢量
的最后一列矢量。用这种方法得到的解矢量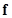 在条件
在条件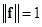 下取
下取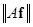 的最小值。
的最小值。
该方法步骤简单,易于实现,但由于其计算结果对输入数据异常敏感,从而直接影响它在实际中的应用。
1997年,Hartley对原始8点算法进行改进,在构造解的方程之前对输入的数据进行适当的归一化。即在形成8点算法的线性方程组之前,图像点的一个简单变换(平移或变尺度)将使这个问题的条件极大地改善,从而提高结果的稳定性。而且进行这种变换所增加的计算复杂性并不显著。算法具体过程具体如下:
- 对原始图象坐标做一个平移变换,使原来以左上角为原点的图象坐标变成以所有图像点的重心为原点的图像坐标;
- 再对图象坐标做一个尺度变换,使得点到原点的平均距离为
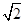 。
。
分别对两幅图像进行以上两步变换,然后将变换后的图像坐标作为输入数据计算基础矩阵。
计算过程如下:
- 设两个独立的图像坐标变换分别为T、
 ,则变换后的图像坐标为
,则变换后的图像坐标为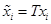 和
和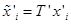 ;
; - 基于转换后的匹配点对
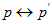 ,利用八点算法计算基础矩阵
,利用八点算法计算基础矩阵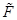 ;
; - 解除归一化,令
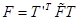 ,矩阵F是对应于原始数据
,矩阵F是对应于原始数据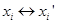 的基本矩阵。
的基本矩阵。
注意:此时求得的F阵的秩并不保证严格为2。而且,由于噪声影响计算得到的F一般都是满秩的。
进而,根据相机的内参信息得到本质矩阵E。
运动恢复
在二视图中,第一个相机的投影矩阵为: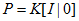 ,而第二个相机的投影矩阵为:
,而第二个相机的投影矩阵为: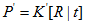 ,投影矩阵的旋转矩阵R和平移矩阵t是要被计算出来的,计算的过程称为运动恢复。这里的“运动”就是第二帧相机相对于第一帧相机的运动变化。
,投影矩阵的旋转矩阵R和平移矩阵t是要被计算出来的,计算的过程称为运动恢复。这里的“运动”就是第二帧相机相对于第一帧相机的运动变化。
1992年,Hartley提出了从本质矩阵在相差一个尺度因子的情况下恢复出摄像机投影矩阵的四个可能解,然后从四个解中选择一个正确解的方法。证明过程可见“计算机视觉中的多视图几何”中文本174页。
定理1:一个3*3的矩阵是本质矩阵的充要条件是它的奇异值中有两个相等而第三个是0。
定理2:设本质矩阵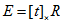 的SVD分解是:
的SVD分解是: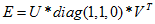 ,不考虑本质矩阵的符号,则存在两种可能的解:
,不考虑本质矩阵的符号,则存在两种可能的解:
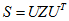 ,
,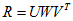
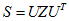 ,
,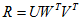
其中:
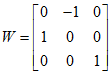
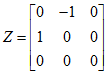
推论:已知本质矩阵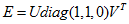 和第一和摄像机矩阵
和第一和摄像机矩阵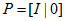 ,那么第二个摄像机矩阵有下列四种可能的选择:
,那么第二个摄像机矩阵有下列四种可能的选择:
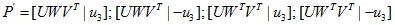
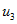 是
是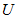 的最后一列。
的最后一列。
t的具体空间长度是不能恢复出来的,只能在相差一个尺度因子的情况下恢复平移单位向量。
4个解的几何解释
显然前面两个解的差别就是第一个摄像机到第二个摄像机的平移矢量是反向的。
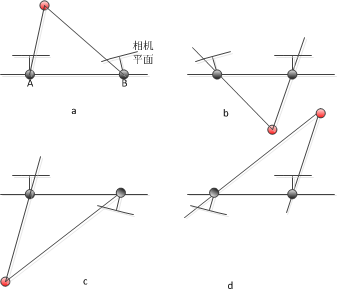
上下两行的差别在于摄像机绕基线旋转了180度,上图中只有(a)时,重构点同时出现在两个摄像机的前面。
从匹配点对中随机选择n对特征点,采用视图重建的方法,分别基于四种可能的摄像机矩阵重建出对应的三维点,满足景深为正的点数最多的解就是对应的,同时也可以确定相机的外参R和t。
本质矩阵E求解及运动状态恢复的更多相关文章
- 2D-2D:对极几何 基础矩阵F 本质矩阵E 单应矩阵H
对极约束 \[ \boldsymbol{x}_{2}^{T} \boldsymbol{F} \boldsymbol{x}_{1}=\boldsymbol{0} \quad \hat{\boldsymb ...
- 【poj3734】矩阵乘法求解
[题意] 给N个方块排成一列.现在要用红.蓝.绿.黄四种颜色的油漆给这些方块染色.求染成红色方块和染成绿色方块的个数同时为偶数的染色方案的个数,输出对10007取余后的答案.(1<=n<= ...
- 【学习笔记】Vins-Mono论文阅读笔记(二)
估计器初始化简述 单目紧耦合VIO是一个高度非线性的系统,需要在一开始就进行准确的初始化估计.通过将IMU预积分与纯视觉结构进行松耦合对齐,我们得到了必要的初始值. 理解:这里初始化是指通过之前imu ...
- SLAM入门之视觉里程计(5):单应矩阵
在之前的博文OpenCV,计算两幅图像的单应矩阵,介绍调用OpenCV中的函数,通过4对对应的点的坐标计算两个图像之间单应矩阵\(H\),然后调用射影变换函数,将一幅图像变换到另一幅图像的视角中.当时 ...
- 多视几何——三角化求解3D空间点坐标
VINS-Mono / VINS-Fusion中triangulatePoint()函数通过三角化求解空间点坐标,代码所体现的数学描述不是很直观,查找资料,发现参考文献[1]对这个问题进行详细解释,记 ...
- CH Round #30 摆花[矩阵乘法]
摆花 CH Round #30 - 清明欢乐赛 背景及描述 艺术馆门前将摆出许多花,一共有n个位置排成一排,每个位置可以摆花也可以不摆花.有些花如果摆在相邻的位置(隔着一个空的位置不算相邻),就不好看 ...
- 学习心得:《十个利用矩阵乘法解决的经典题目》from Matrix67
本文来自:http://www.matrix67.com/blog/archives/tag/poj大牛的博文学习学习 节选如下部分:矩阵乘法的两个重要性质:一,矩阵乘法不满足交换律:二,矩阵乘法满足 ...
- Android自己定义控件——3D画廊和图像矩阵
转载请注明出处:http://blog.csdn.net/allen315410/article/details/39932689 1.3D画廊的实现 我们知道android系统已经为我们提供好了一个 ...
- 【转】Matrix67:十个利用矩阵乘法解决的经典题目
好像目前还没有这方面题目的总结.这几天连续看到四个问这类题目的人,今天在这里简单写一下.这里我们不介绍其它有关矩阵的知识,只介绍矩阵乘法和相关性质. 不要以为数学中的矩阵也是黑色屏幕上不断变化的 ...
随机推荐
- webpack window 使用sass来编译css样式
1.执行安装: npm install sass-loader --save-dev (此处不行的话就换上npm install node-sass) 2.稍微修改一下config,删掉我们先前添加的 ...
- 【Spring】Spring之向 IOC 容器注入对象的三种方式
关于Spring的搭建可参见:浅析Spring框架的搭建.在测试之前还是应该先将环境配置好,将相关Jar包导进来.Spring创建的对象,默认情况下都是单例模式,除非通过scope指定. 向IOC容器 ...
- App Icon Gear App 图标制作工具
1.App Icon Gear 简介 App Icon Gear(原名 AppIconMaker)不仅可以创建 App 图标.启动图 LaunchImage,还可以生成自定义尺寸的图标集(Image ...
- appium简明教程(9)——如何获取android app的Activity
有时候在appium的Desired Capabilities中需要指定被测app的appActivity,下面的方法可能会对你有所帮助. 方法一 如有你有待测项目的源码,那么直接查看源码就好.如果没 ...
- SQL 正则表达式 `(user_log_acct)?+.+`
SELECT 语句可以使用正则表达式做列选择,下面的语句查询除了 ds 和 hr 之外的所有列: SELECT `(ds|hr)?+.+` FROM test
- uiautomatorviewer 查看元素新思路
用adb 命令把图片和uix获取出来,再导入uiautomatorviewer adb shell uiautomator dump /data/local/tmp/uidump.uixadb pul ...
- Mac下 如何配置虚拟机软件Parallel Desktop--超详细
Mac下 如何配置虚拟机软件Pparallel Desktop--超详细 Mac 的双系统解决方案有两种,一种是使用Boot Camp分区安装独立的Windows,一种是通过安装Parallels D ...
- CentOS下配置redis允许远程连接
1. 目的 因为想要学习redis,因此在虚拟机中安装了redis,为了实现在物理机可以访问redis,弄了好久:因此记录下来,以免忘记. 2. 环境 虚拟机:CentOS Linux release ...
- 有用的 Mongo命令行 db.currentOp() db.collection.find().explain() - 摘自网络
在Heyzap 和 Bugsnag 我已经使用MongoDB超过一年了,我发现它是一个非常强大的数据库.和其他的数据库一样,它有一些缺陷,但是这里有一些东西我希望有人可以早一点告诉我的. 即使建立索引 ...
- jQueryUI modal dialog does not show close button (x) JQueryUI和BootStrap混用时候,右上角关闭按钮显示不出图标的解决办法
I had this problem and was able to resolve it with the declaration below. $.fn.bootstrapBtn = $.fn.b ...
