boosting方法

概述

Boosting基本思想: 通过改变训练数据的概率分布（训练数据的权值分布），学习多个弱分类器，并将它们线性组合，构成强分类器。

Boosting算法要求基学习器能对特定的数据分布进行学习，这可通过“重赋权法”（re-weighting）实施。对无法接受带权样本的基学习算法，则可通过“重采样法”（re-sampling）来处理。若采用“重采样法”，则可获得“重启动”机会以避免训练过程过早停止。可根据当前分布重新对训练样本进行采样，再基于新的采样结果重新训练处基学习器。

提升方法AdaBoost算法

1、提升方法的基本思路

（1）提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。未被正确分类的样本受到后一轮弱分类器更大的关注。
（2）AdaBoost 采用加权多数表决，加大分类误差率小的弱分类器的权值，使其在表决中起较大的作用。

2、AdaBoost算法

注意：修改：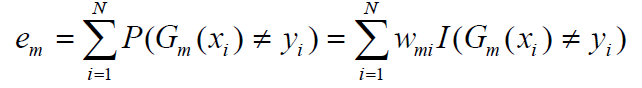

3、一个例子

AdaBoost算法的训练误差分析

AdaBoost算法的解释

1.前向分布算法

2、前向分布算法与AdaBoost算法

AdaBoost算法可以由前向分布算法推导得出，主要依据如下定理：

证明参考这位大神：https://blog.csdn.net/thriving_fcl/article/details/50877957

证明太精彩了，唯一不明白就是样本权值更新公式。

提升树

1、提升树模型

提升树模型可以表示为决策树的加法模型：

其中，

2、提升树算法

用平方误差损失函数的回归问题，用指数损失函数的分类问题，以及用一般损失函数的一般决策问题。

（1）分类问题同上面说过的例子，基分类器换做决策树就行了。下面看一下回归问题：

（2）一个例子

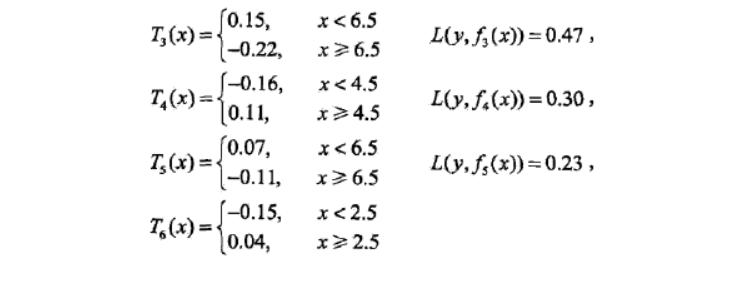
3、梯度提升

总而言之

最后小结一下GBDT算法的优缺点。

优点：

• 预测精度高
• 适合低维数据
• 能处理非线性数据

缺点：

• 并行麻烦（因为上下两棵树有联系）
• 如果数据维度较高时会加大算法的计算复杂度