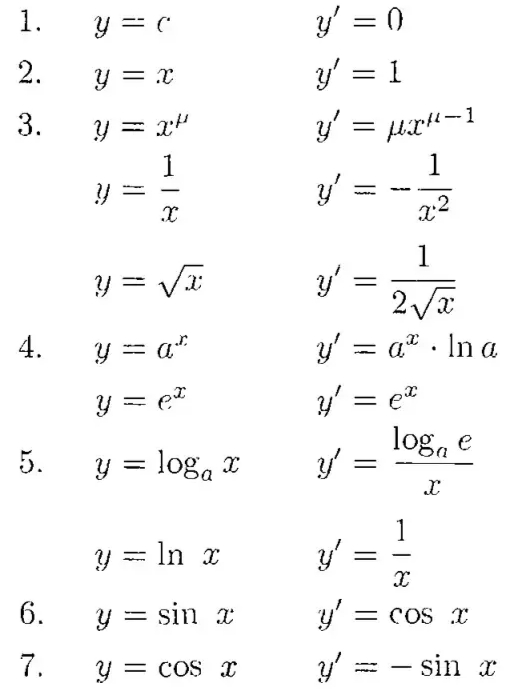SciTech-Mathmatics-Analysis-Calculus: Difference+Derivative+Integral+Limit:极限(变化测度与量化,高阶)+Series无穷级数+Field:Closure+Theories{RealTheory:Continuity+Measure:Metric+Set(Countability,Set Vs. Element-Wise)}

SciTech-Mathmatics-Analysis

Mathematical Thinking

数学思维：集合论，数和数域，运算符号，函数关系，数形结合；

导数、微分、积分的奥秘就在(例如变形：同一公式换一种形式表达, 就是另一种用途)：

• 微分升幂：将"静态/结果"的 "点值"/"线段"和"维度函数(定义域:整个数轴+零点偏移)" 变换为 "动态/过程" 的 "无穷级数".
• 求导降幂：将 "动态/过程" 的 "点值"/"线段"和"维度函数(定义域:整个数轴+零点偏移)" 分解出 静态/结果 的规律.

• \(\large f'(x) = dy / dx\)

• \(\large dy = f'(x) dx\)

• the Definite Difference:
  
  \(\large \begin{array}{rll} \int_{a}^{b}{f'(x) dx} =& \underset{n \rightarrow \infty}{\lim} \overset{ n }{\underset{k=1}{\sum}} { \Delta{f(x_k)} } & \leftarrow \ 微分划分形 \\
  =& \underset{n \rightarrow \infty}{\lim} \overset{n}{\underset{k=1}{\sum}} { ( f'(x_k) \cdot \Delta{x_k} ) } & \leftarrow \ Riemman's\ Sum\ Form \\
  =& f(b) - f(a) & \leftarrow \ 积分化差形 \\
  \end{array}\)

• the Indefinite Integral:
  
  \(\large \begin{array}{rll} \\
  \int{f'(x) dx} &= f(x) + C & \ f'(x)dx 整体是被积表达式;\ f'(x)只是被积函数. & \\
  Definite &\rightarrow Indefinite & [a,b]扩展到[-\infty, +\infty]; 积分值由f(b) - f(a), 变换为 f(x) + C(不定常数). & \\
  \end{array}\)

• 导数与微分:
  
  \(\large f'(x) = dy / dx\) 即 \(\large dy = f'(x) dx\)

  • 升幂：
    
    将“点值”、“线段”和“整个数轴+零点偏移”用“无穷级数”形式表示。

    • \(\large dN= 0 dx\), \(\large y = X,\ X \in R\)
      
      常数函数的 导函数的值总是0
    • \(\large dx = 1 dx\), \(\large y = kx + b,\ k \in R, \ b \in R\)
      
      线性函数 的导函数的值为常数 \(\large k\)
      
      更特别是\(\large y = x\)的导数值为1
    • \(\large d{x^n} = n x^{n- 1}dx\)
      
      幂函数每乘一次\(\large dx\) 可以升幂指数一级

  • \(\large d{e^x} = e^x dx\), $\large d{n^x} = d{e^{x ln{n}}} = e^{x ln{n}} d({x ln{n}}) = n^x\ ln{n}\ dx $
    
    自然数 指数函数 的导函数值为其本身, 自然数 指数函数

  • \(\large d({ln {x}}) = \frac{1}{x} dx\),
    
    自然数 对数函数 的导函数为\(\large \frac{1}{x}\), 自然数为底数的 对数函数。

  • 常用函数，及其导函数表
    
    

Calculus: 微积分

变化: relation, measurement度量，规律:

• 数学分析：“无穷无尽”是研究对象，“极限”是“研究方法”；
  
  用 "n项数列(n是可变项数)" 和 "无穷级数", 在"确定项数" 与 "无穷或不确定的项数"之间，
  
  用"极限"建立"量变与质变"的"函数关系"。

• Difference微分 与 Derivative导数：
  
  measurement, 极限, approximation

• Derivative导数 与 Integral积分 互为逆运算：

  • 由“导数”求“原函数” ；
  • 由“原函数”求“导数”；

• 多重微分 Vs. 积分角度:
  
  多重微分 是 将 一维的函数值域(常为R)分解到 "确定的多维度自变量域"上的 "函数(关系与测度)表示"
  
  多重积分 是 用 "多维度的自变量域"的 "函数(关系与测度)表示" 合成一维的函数值域(常为R).

Derivative导数

\(\large \begin{array}{rl} \\
f'(x) &= \underset{\Delta{x}\rightarrow 0}{\lim}{ \frac{\Delta{y}}{\Delta{x}} } \\
&= \underset{\Delta{x}\rightarrow 0}{\lim}{ \frac{ f(x + \Delta{x}) - f(x) }{\Delta{x}} } \\
&= \underset{\Delta{x}\rightarrow 0}{\lim}{( f'(x)+ O(\Delta{x}) )} \\
&= f'(x) \\
\end{array}\)

常用函数及其导函数：

\(\large \begin{array}{rl} \\
f(x)=x^n, & f'(x) = n x^{n-1} \\
f(x)=e^x, & f'(x) = e^x \\
f(x)=ln{x}, & f'(x) = \frac{1}{x} \\
f(x)=\sin{x}, & f'(x) = \cos{x} \\
f(x)=\cos{x}, & f'(x) = - \sin{x} \\
\end{array}\)

Difference微分：

• 一重微分
  
  \(\large \begin{array}{rl} \\
  \Delta{y} &= \underset{\Delta{x}\rightarrow 0}{\lim}{ f(x + \Delta{x}) - f(x) } \\
  &= \underset{\Delta{x}\rightarrow 0}{\lim}{ f'(x) \cdot \Delta{x} + O(\Delta{x}) } \\
  &= \underset{\Delta{x}\rightarrow 0}{\lim}{ f'(x) \cdot \Delta{x} } \\
  \end{array}\)
• N重微分
  
  多重微分 是 将 一维的函数值域(常为R)分解到 "确定的正交多维度自变量域"上的 "函数(关系与测度)表示"；
  
  例如求不规则体的体积：是微分到(x, y, z)三个纬度上；

Integral积分

• 一重积分:

  • Riemman Integral 定积分:
    
    \(\large \begin{array}{rl} \\
    \int_{a}^{b}{f'(x) dx} =& f(b) - f(a) \\
    =& \underset{n \rightarrow \infty}{\lim} \overset{ n }{\underset{k=1}{\sum}} { ( f'(x_k) \cdot \Delta{x_k} ) }, 黎曼和形式\\
    =& \underset{n \rightarrow \infty}{\lim} \overset{ n }{\underset{k=1}{\sum}} { \Delta{f(x_k)} } \\
    =& \underset{n \rightarrow \infty}{\lim} \overset{ n }{\underset{k=1}{\sum}} {( f(x_{k}) - f(x_{(k-1)}) )} \\
    =& \underset{n \rightarrow \infty}{\lim} ( f(x_{1}) - f(a) + f(x_{2}) - f(x_{1}) + \cdots + f(b) - f(x_{n-1}) ) \\
    where: & \\
    k \in & [1, n] \\
    \end{array}\)

  • 不定积分:
    
    \(\large \begin{array}{rl} \\
    \int{f'(x) dx} =& f(x) + C \\
    where: & \\
    C :& 是一积分常数; \\
    \int :& 积分号; \\
    x :& 积分变量; \\
    f'(x) :& 被积函数; \\
    f'(x)dx :& 被积表达式; \\
    \end{array}\)

• 多重积分:
  
  多重积分 是 用 "正交多维度的自变量域"上的 "函数(关系与测度)表示" 合成一维的函数值域(常为R)。

Limit:极限(变化的测度与量化,高阶 )

• 数学分析: 变化与无穷 是 研究对象, 函数与极限 是“研究方法”
  
  用 "n项数列(n是可变项数)" 和 "无穷级数", 在"确定项数" 与 "无穷或不确定的项数"之间，
  
  用"极限"建立"量变与质变"的"函数关系"。
  
  例如: \(\large f'(x) = \underset{\Delta{x}\rightarrow 0}{\lim}{ \frac{\Delta{y}}{\Delta{x}} } = \underset{\Delta{x}\rightarrow 0}{\lim}{ \frac{ f(x + \Delta{x}) - f(x) }{\Delta{x}} }\)

  • 在 \(\large \Delta{x}\rightarrow 0\)时，$\large \Delta{y} $ 与 $\large \Delta{x} $ 都是变化量；
  • 变化的“快慢”是Relatively Measurable, and can be Quantified by Derivatives, High-order Derivatives and High-order Differences.

• 导数值就是value of relatively mesurement , 规律性。
  
  导函数则是，总体的“变化快慢”的度量函数；

• 高阶无穷小: $\large \underset{\Delta{x}\rightarrow 0}{\lim} { O(\Delta{x}) } = 0 $

  • 高阶无穷小 在“自变量取极限时”为0，规律性。
    • "0(是在Real line上任取一点设置为0)",
    • "无穷小\(\large \epsilon\)"的度量, 函数关系\(\large \delta\), 运算法则(线性) 以及 极限；
  • 类似，无穷小的倒数则是 $\large \infty $
  • 无穷小 的运算规律。

• Series数列/无穷级数:

  • 数, a point in real line, can be represented as an infinity series.
  • 数列, 等差，等比，求和公式；
  • 无穷级数；
  • Cauchy Series

• Field:数域(Closure),

  • Rational Number,
    • 稠密性:任两个不同Rationals之间有无尽的Rationals
      
      例如 c = (a+b)/2;
    • 阿基米德性
  • Real Number:
    • FOC(field, order, continuity) Axioms
    • Continuity(Completeness)
  • Complex Number,
    • \(\large i = \sqrt{-1}\),
    • 迪莫佛定理: $\large e^{i\alpha} \cdot e^ {i\beta} = e ^{i(\alpha+\beta)} $,
    • Euler's Equation: \(\large e^{i\theta} = \cos{\theta} + i \cdot \sin{\theta},\ \theta \in \bm{C}\),
      
      \(\large let\ \theta = \pi,\ then\ e^{i\pi} + 1 = 0\),
    • Taylor equation in Complex Field.

• Number Theory数论:

  • Primes:
    
    \(\large Euler's\ proof\) for "\(\large \text{ There are infinite number of Primes. }\)":
    
    \(\large (P_1 \cdot P_2 \cdot \cdots \cdot P_n + 1) \ is\ a\ prime, if\ P_i \ are\ continued\ primes\ serie\ from\ 1, \ i \in [1,\ n]\)
  • Factorization(因式分解):
    
    $\large \forall\ i \in N, \exists\ unique\ representation\ i = P_1^{n_1} \cdot P_2^{n_2} \cdot P_k^{n_k} $
  • Functions: 121 mapping, bijection;

• RealNumberTheory:实数理论

  • 连续Continuity/完备Completeness:
    • Dedkind Split: 不空、不漏、不乱
    • 闭区间套
  • fractions(小数论):
    • Rational fractions: 最小数域;
    • Irrational fractions: 无理数, 无限不循环小数；\(\large \pi,\ e,\ \sqrt{2}\)

• Probability Theory概率论
  
  Probability

• MeasureTheory测度论
  
  Triangle Equation
  
  Metric

• SetTheory集合论(Countable/Uncountable, 可列可加)

  • Set Vs. Element:
    • Set/Collection is collective object, or a "line, circle, square, rectangle"
    • Element is considered as individual object. or a "point";
  • Operations:
    • Set-wise operations is cooresponding to and driving by Element-wise operations.