ARC165F题解

前言

\(2024.10.19\) 日校测 \(T4\)，思维太庙，被薄纱了，遂哭弱，写题解以记之。

简要题意

给你一个长度为 \(2n\) 的序列满足 \(\forall a_i\in[1,n]\)，其中 \(1\) 到 \(n\) 每个数都出现了两次，现在需要把相同的两个数排到一起，每次操作只能交换相邻两个数，在保证操作次数最小的情况下求出现在序列的最小字典序。

数据范围：\(1\le n\le2\times10^5\)。

思路

做题的时候首先应该考虑题目性质，可以从手玩样例开始。因为最后并没有让你求最少操作次数，所以我们只用讨论数与数之间的关系。我们考虑最简单的情况：假设现在序列中只有 \(1\) 和 \(2\) 各两个，一共存在六种可能的情况。我们先将他们列出来：

1. \(1122\)
2. \(1212\)
3. \(1221\)
4. \(2112\)
5. \(2121\)
6. \(2211\)

对于第一种和第六种情况我们可以不用考虑，因为需要保证操作数最小。然后这四种情况实际只有两种本质不同，我们将他们抓出来。假设有两数 \(A,B\) 位置关系如下：

• \(ABAB\)
• \(ABBA\)

对于第一个情况，我们只需将中间两数交换即可。而第二种，我们既可以将第一个数交换到第三个位置，也可以将最后一个数交换到第二个位置。也就是说：第一种情况下数的位置决定最后顺序；而第二种情况下数的大小决定了最后顺序。

现在考虑扩展这两种情况，对于数列中任意的两数 \(A,B\)，如果满足 \(A\dots B\dots A\dots B\) 的形式，我一定会让 \(A\) 排在 \(B\) 前面；如果满足 \(A\dots B\dots B\dots A\) 的形式，我就会去考虑两个数之间的大小关系。

总结一下：

\(\forall x\in[1,n]\)，设 \(a_x\) 表示其第一次出现的位置，\(b_x\) 表示第二次出现的位置，如满足偏序：\(a_i\le a_j,b_i\le b_j\) 则 \(i\) 在 \(j\) 之前。所以把这些偏序抽象成一张图跑拓扑排序，拓扑时让数字小的点尽量先跑就能满足第二种情况。

可是直接建图跑是 \(O(n^2)\) 的，考虑优化。我们把每一个关于 \(i\) 的二元组 \((a_i,b_i)\) 看成平面内的点，若 \(i,j\) 之间连边则需要满足上述偏序。我们可以考虑分治建图，也就是类似 \(\text{cdq}\) 的过程，具体见下图：

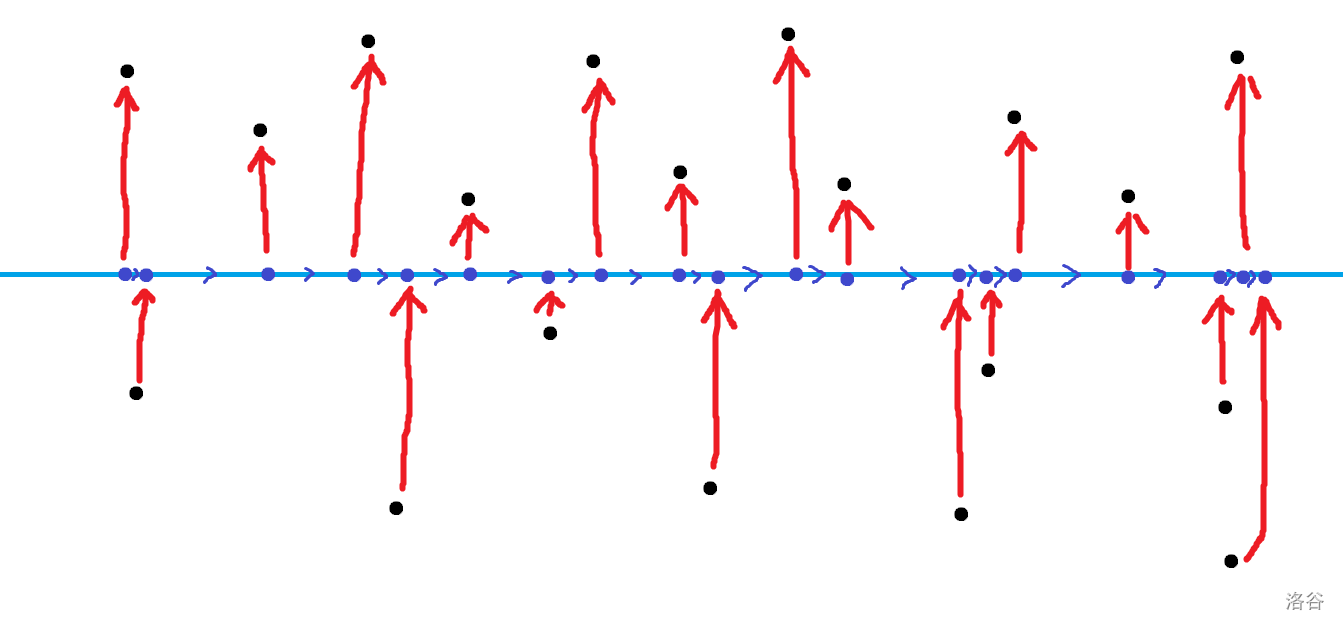
我们横着切一刀把平面分成两部分，在分割线上建一些虚点。对于下面的实点垂直向上连边，上面的实点从下面虚点往上连边，然后虚点之间从左往右连。若每次在中间切最多切出 \(\log n\) 层，所以只有 \(n\log n\) 个点和边。但是拓扑的时候如果用优先队列是两只 \(\log\) 的，考虑继续优化。

其实我们只需要对实点用优先队列，对于虚点我们不关心他们的具体顺序，所以开一个普通队列存虚点，另一个优先队列存实点，每次先把所有普通队列的点拓扑完再去拓扑优先队列就行。时间复杂度是 \(O(n\log n)\) 的，因为实点只有 \(n\) 个。

代码

void cdq(int l, int r){
	if(l == r)return; int mid = l + r >> 1, lim = a[mid].l;
	cdq(l, mid), cdq(mid + 1, r);
	int i = l, j = mid + 1, k = l;
	while(i <= mid and j <= r)a[i].r < a[j].r ? b[k++] = a[i++] : b[k++] = a[j++];
	while(i <= mid)b[k++] = a[i++]; while(j <= r)b[k++] = a[j++];
	for(int i = l; i <= r; ++i){
		a[i] = b[i], ++nd; if(i ^ l)e[nd - 1].pb(nd), ++in[nd];
		if(a[i].l <= lim)e[a[i].id].pb(nd), ++in[nd];
		else e[nd].pb(a[i].id), ++in[a[i].id];
	}
}
void upd(int x){
	if(in[x])return;
	x <= n ? q.push(x) : qc.push(x);
}

signed main(){
	freopen("swap.in", "r", stdin);
	freopen("swap.out", "w", stdout);
	n = rd(), nd = n << 1;
	for(int i = 1; i <= nd; ++i){
		int x = rd();
		if(a[x].l)a[x].r = i; else a[x].l = i, a[x].id = x;
	}
	sort(a + 1, a + 1 + n); nd = n;
	cdq(1, n);
	for(int i = 1; i <= nd; ++i)upd(i);
	while(! q.empty() or ! qc.empty()){
		while(! qc.empty()){
			int u = qc.front(); qc.pop();
			for(int v : e[u])--in[v], upd(v);
		}
		if(q.empty())return 0;
		int u = q.top(); q.pop();
		pc(u), putchar(' '), pc(u), putchar(' ');
		for(int v : e[u])--in[v], upd(v);
	}
	return 0;
}