GAMES103 FEM 有限元模拟弹性房子
简介
有限元方法, 把物体分割成一个个有体积的单元来模拟.
线性有限元方法在二维空间中把物体分割成三角形/四边形, 在三维空间中把物体分割成四面体/六面体.
有限元方法由能量对位置求导得到力,有限体积方法对 traction vector 积分得到力。
TIPS
STVK模型, PPT中写错了, 正确的在 https://www.bilibili.com/read/cv14754926 上有讲解
\]
核心参考PPT
SVTK实现
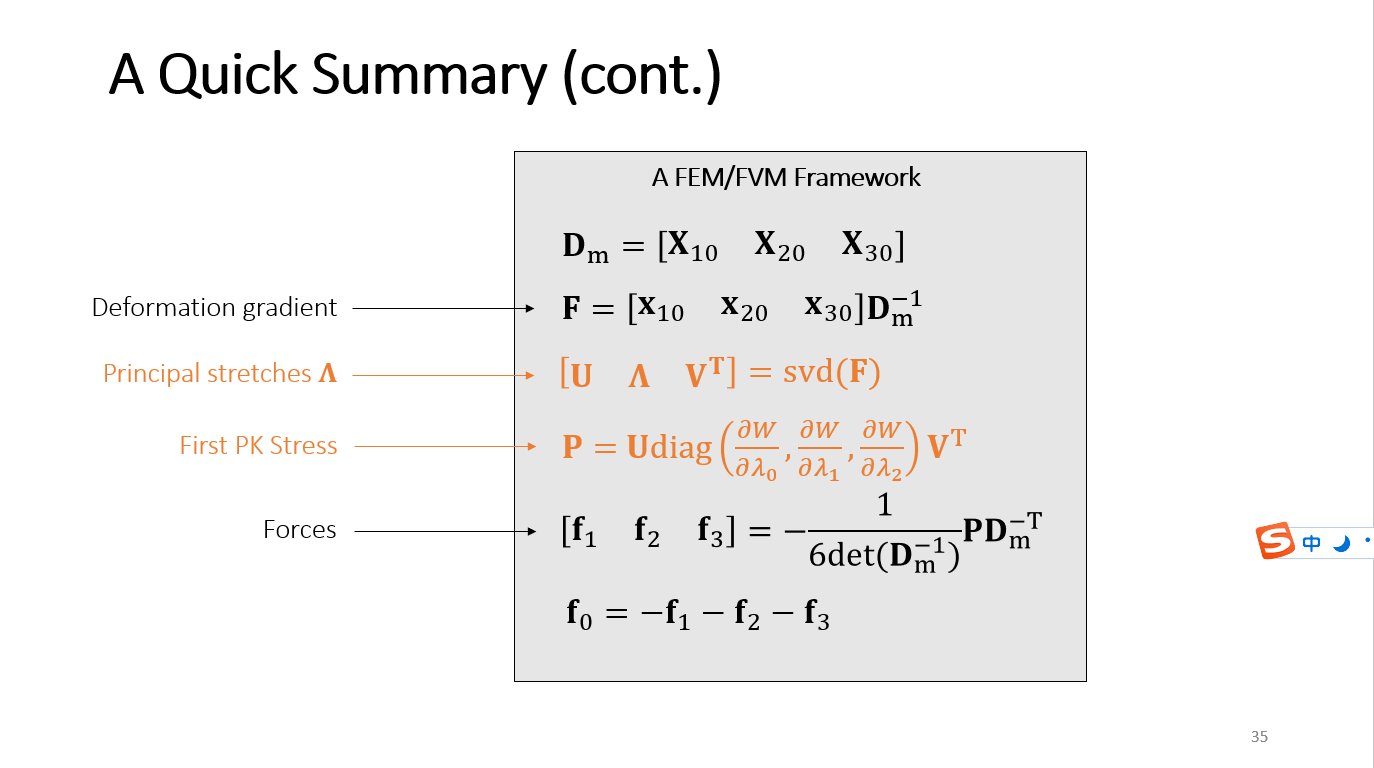
FVM实现, 说实话 我也不知道 下面实现的是有限元还是有限体积, 逻辑上应该是有限体积

关于Laplacian 速度平滑
就是V_SUM 周围顶点速度的和
V_NUM 周围顶点的个数
附录: 师弟代码
code
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using System;
using System.IO;
public class FVM : MonoBehaviour
{
float dt = 0.003f;
float mass = 1;
float stiffness_0 = 7500.0f;
float stiffness_1 = 5000.0f;
float damp = 0.999f;
float Un = 0.5f; // for collision
float Ut = 0.5f; // for collision
Vector3 P = new Vector3(0, -3, 0);
Vector3 N = new Vector3(0, 1, 0);
int[] Tet; //四面体数据
int tet_number; //The number of tetrahedra 四面体数目
Vector3[] Force; //力
Vector3[] V; //速度
Vector3[] X; //点数据
int number; //The number of vertices
Matrix4x4[] inv_Dm;
//For Laplacian smoothing.
Vector3[] V_sum;
int[] V_num;
SVD svd = new SVD();
// Start is called before the first frame update
void Start()
{
// FILO IO: Read the house model from files.
// The model is from Jonathan Schewchuk's Stellar lib.
{
string fileContent = File.ReadAllText("Assets/house2.ele");
string[] Strings = fileContent.Split(new char[] { ' ', '\t', '\r', '\n' }, StringSplitOptions.RemoveEmptyEntries);
tet_number = int.Parse(Strings[0]);
Tet = new int[tet_number * 4];
for (int tet = 0; tet < tet_number; tet++)
{
Tet[tet * 4 + 0] = int.Parse(Strings[tet * 5 + 4]) - 1;
Tet[tet * 4 + 1] = int.Parse(Strings[tet * 5 + 5]) - 1;
Tet[tet * 4 + 2] = int.Parse(Strings[tet * 5 + 6]) - 1;
Tet[tet * 4 + 3] = int.Parse(Strings[tet * 5 + 7]) - 1;
}
}
{
string fileContent = File.ReadAllText("Assets/house2.node");
string[] Strings = fileContent.Split(new char[] { ' ', '\t', '\r', '\n' }, StringSplitOptions.RemoveEmptyEntries);
number = int.Parse(Strings[0]);
X = new Vector3[number];
for (int i = 0; i < number; i++)
{
X[i].x = float.Parse(Strings[i * 5 + 5]) * 0.4f;
X[i].y = float.Parse(Strings[i * 5 + 6]) * 0.4f;
X[i].z = float.Parse(Strings[i * 5 + 7]) * 0.4f;
}
//Centralize the model.
Vector3 center = Vector3.zero;
for (int i = 0; i < number; i++) center += X[i];
center = center / number;
for (int i = 0; i < number; i++)
{
X[i] -= center;
float temp = X[i].y;
X[i].y = X[i].z;
X[i].z = temp;
}
}
/*tet_number=1;
Tet = new int[tet_number*4];
Tet[0]=0;
Tet[1]=1;
Tet[2]=2;
Tet[3]=3;
number=4;
X = new Vector3[number];
V = new Vector3[number];
Force = new Vector3[number];
X[0]= new Vector3(0, 0, 0);
X[1]= new Vector3(1, 0, 0);
X[2]= new Vector3(0, 1, 0);
X[3]= new Vector3(0, 0, 1);*/
//Create triangle mesh.
Vector3[] vertices = new Vector3[tet_number * 12];
int vertex_number = 0;
for (int tet = 0; tet < tet_number; tet++)
{
vertices[vertex_number++] = X[Tet[tet * 4 + 0]];
vertices[vertex_number++] = X[Tet[tet * 4 + 2]];
vertices[vertex_number++] = X[Tet[tet * 4 + 1]];
vertices[vertex_number++] = X[Tet[tet * 4 + 0]];
vertices[vertex_number++] = X[Tet[tet * 4 + 3]];
vertices[vertex_number++] = X[Tet[tet * 4 + 2]];
vertices[vertex_number++] = X[Tet[tet * 4 + 0]];
vertices[vertex_number++] = X[Tet[tet * 4 + 1]];
vertices[vertex_number++] = X[Tet[tet * 4 + 3]];
vertices[vertex_number++] = X[Tet[tet * 4 + 1]];
vertices[vertex_number++] = X[Tet[tet * 4 + 2]];
vertices[vertex_number++] = X[Tet[tet * 4 + 3]];
}
int[] triangles = new int[tet_number * 12];
for (int t = 0; t < tet_number * 4; t++)
{
triangles[t * 3 + 0] = t * 3 + 0;
triangles[t * 3 + 1] = t * 3 + 1;
triangles[t * 3 + 2] = t * 3 + 2;
}
Mesh mesh = GetComponent<MeshFilter>().mesh;
mesh.vertices = vertices;
mesh.triangles = triangles;
mesh.RecalculateNormals();
V = new Vector3[number];
Force = new Vector3[number];
V_sum = new Vector3[number];
V_num = new int[number];
for (int tet = 0; tet < tet_number; tet++)
{
V_num[Tet[tet * 4]] += 4;
V_num[Tet[tet * 4 + 1]] += 4;
V_num[Tet[tet * 4 + 2]] += 4;
V_num[Tet[tet * 4 + 3]] += 4;
}
//TODO: Need to allocate and assign inv_Dm
inv_Dm = new Matrix4x4[tet_number];
for (int tet = 0; tet < tet_number; tet++)
{
inv_Dm[tet] = Build_Edge_Matrix(tet).inverse;
//Debug.Log("inv_Dm:" + inv_Dm[tet]);
}
}
Matrix4x4 Build_Edge_Matrix(int tet)
{
Matrix4x4 ret = Matrix4x4.zero;
//TODO: Need to build edge matrix here.
ret[0, 0] = X[Tet[tet * 4]][0] - X[Tet[tet * 4 + 1]][0];
ret[1, 0] = X[Tet[tet * 4]][1] - X[Tet[tet * 4 + 1]][1];
ret[2, 0] = X[Tet[tet * 4]][2] - X[Tet[tet * 4 + 1]][2];
ret[0, 1] = X[Tet[tet * 4]][0] - X[Tet[tet * 4 + 2]][0];
ret[1, 1] = X[Tet[tet * 4]][1] - X[Tet[tet * 4 + 2]][1];
ret[2, 1] = X[Tet[tet * 4]][2] - X[Tet[tet * 4 + 2]][2];
ret[0, 2] = X[Tet[tet * 4]][0] - X[Tet[tet * 4 + 3]][0];
ret[1, 2] = X[Tet[tet * 4]][1] - X[Tet[tet * 4 + 3]][1];
ret[2, 2] = X[Tet[tet * 4]][2] - X[Tet[tet * 4 + 3]][2];
ret[3, 3] = 1;
return ret;
}
Matrix4x4 M_Division(Matrix4x4 m, float scale)
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
m[i, j] /= scale;
}
}
return m;
}
Matrix4x4 M_Multipy(Matrix4x4 m, float scale)
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
m[i, j] *= scale;
}
}
return m;
}
Matrix4x4 M_addtion(Matrix4x4 m1, Matrix4x4 m2)
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
m1[i, j] += m2[i, j];
}
}
return m1;
}
Matrix4x4 M_Dec(Matrix4x4 m1, Matrix4x4 m2)
{
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
m1[i, j] -= m2[i, j];
}
}
return m1;
}
float TR(Matrix4x4 m)
{
float res = 0f;
res += m.m00;
res += m.m11;
res += m.m22;
return res;
}
void Update_Collision_Point(int idx, float distance, Vector3 N)
{
X[idx] -= distance * N;
float viN = Vector3.Dot(V[idx], N);
if (viN >= 0) return;
Vector3 v_Ni = viN * N; // (vi * N)N 反弹面的分量
Vector3 v_Ti = V[idx] - v_Ni; // 沿着面的分量
//定义摩擦系数a
float a = Mathf.Max(1.0f - Ut * (1.0f + Un) * v_Ni.magnitude / v_Ti.magnitude, 0.0f);
//计算新速度
Vector3 v_Ni_new = -Un * v_Ni;
Vector3 v_Ti_new = a * v_Ti;
V[idx] = v_Ni_new + v_Ti_new;
}
Matrix4x4 SVtk(Matrix4x4 F)
{
Matrix4x4 P = Matrix4x4.zero;
Matrix4x4 U = Matrix4x4.zero;
Matrix4x4 S = Matrix4x4.zero;
Matrix4x4 V = Matrix4x4.zero;
Matrix4x4 Plamda = Matrix4x4.zero;
svd.svd(F, ref U, ref S, ref V);
float lamda0 = S[0, 0];
float lamda1 = S[1, 1];
float lamda2 = S[2, 2];
float Ic = lamda0 * lamda0 + lamda1 * lamda1 +
lamda2 * lamda2;
float Ic_l0 = 2f * lamda0;
float Ic_l1 = 2f * lamda1;
float Ic_l2 = 2f * lamda2;
//float IIc_l0 = 2f * lamda0 * (lamda1 * lamda1 + lamda2 * lamda2);
//float IIc_l1 = 2f * lamda1 * (lamda0 * lamda0 + lamda2 * lamda2);
//float IIc_l2 = 2f * lamda2 * (lamda1 * lamda1 + lamda0 * lamda0);
float IIc_l0 = 4f * lamda0 * lamda0 * lamda0;
float IIc_l1 = 4f * lamda1 * lamda1 * lamda1;
float IIc_l2 = 4f * lamda2 * lamda2 * lamda2;
//float IIc_l0 = 4f * lamda0 * lamda0 * lamda0 * lamda1 * lamda1 * lamda1 * lamda1 * lamda2 * lamda2 * lamda2 * lamda2;
//float IIc_l1 = 4f * lamda1 * lamda1 * lamda1 * lamda0 * lamda0 * lamda0 * lamda0 * lamda2 * lamda2 * lamda2 * lamda2;
//float IIc_l2 = 4f * lamda2 * lamda2 * lamda2 * lamda1 * lamda1 * lamda1 * lamda1 * lamda0 * lamda0 * lamda0 * lamda0;
Plamda[0, 0] = stiffness_0 * (Ic - 3f) * Ic_l0 /4f +
stiffness_1 * (IIc_l0 - 2 * Ic_l0) / 4f;
Plamda[1, 1] = stiffness_0 * (Ic - 3f) * Ic_l1 /4f +
stiffness_1 * (IIc_l1 - 2 * Ic_l1) / 4f;
Plamda[2, 2] = stiffness_0 * (Ic - 3f) * Ic_l2 /4f +
stiffness_1 * (IIc_l2 - 2 * Ic_l2) / 4f;
Plamda[3, 3] = 1f;
P = U * Plamda * V.transpose;
return P;
}
void _Update()
{
// Jump up.
if (Input.GetKeyDown(KeyCode.Space))
{
for (int i = 0; i < number; i++)
V[i].y += 0.2f;
}
for (int i = 0; i < number; i++)
{
//TODO: Add gravity to Force.
Force[i] = new Vector3(0, -9.8f, 0);
}
for (int tet = 0; tet < tet_number; tet++)
{
Matrix4x4 I = Matrix4x4.identity;
//TODO: Deformation Gradient
Matrix4x4 F = Build_Edge_Matrix(tet);
F = F * inv_Dm[tet];
//TODO: Green Strain
Matrix4x4 G = M_Division(M_Dec(F.transpose * F, I)
, 2f);
//TODO: Second PK Stress
Matrix4x4 S = M_addtion(M_Multipy(G,
stiffness_1 * 2f), M_Multipy(I, TR(G) *
stiffness_0));
Matrix4x4 P = F * S;
//SVTK
P = SVtk(F);
//TODO: Elastic Force
Matrix4x4 EF = M_Multipy(P * (inv_Dm[tet].transpose)
, -1f / (6f * inv_Dm[tet].determinant));
//Debug.Log("EF:" + EF);
Force[Tet[tet * 4 + 1]][0] += EF[0, 0];
Force[Tet[tet * 4 + 1]][1] += EF[1, 0];
Force[Tet[tet * 4 + 1]][2] += EF[2, 0];
Force[Tet[tet * 4 + 2]][0] += EF[0, 1];
Force[Tet[tet * 4 + 2]][1] += EF[1, 1];
Force[Tet[tet * 4 + 2]][2] += EF[2, 1];
Force[Tet[tet * 4 + 3]][0] += EF[0, 2];
Force[Tet[tet * 4 + 3]][1] += EF[1, 2];
Force[Tet[tet * 4 + 3]][2] += EF[2, 2];
Force[Tet[tet * 4]][0] += -EF[0, 0] - EF[0, 1] - EF[0, 2];
Force[Tet[tet * 4]][1] += -EF[1, 0] - EF[1, 1] - EF[1, 2];
Force[Tet[tet * 4]][2] += -EF[2, 0] - EF[2, 1] - EF[2, 2];
}
for (int i = 0; i < number; i++)
{
//TODO: Update X and V here.
V[i] += Force[i] * dt;
V[i] *= damp;
X[i] += V[i] * dt;
//TODO: (Particle) collision with floor.
float distance = Vector3.Dot(X[i] - P, N);
if (distance < 0)
{
Update_Collision_Point(i, distance, N);
}
V_sum[i] = Vector3.zero;
}
//laplacian
for (int tet = 0; tet < tet_number; tet++)
{
Vector3 v0 = V[Tet[tet * 4]];
Vector3 v1 = V[Tet[tet * 4 + 1]];
Vector3 v2 = V[Tet[tet * 4 + 2]];
Vector3 v3 = V[Tet[tet * 4 + 3]];
Vector3 vs = v0 + v1 + v2 + v3;
V_sum[Tet[tet * 4]] += vs;
V_sum[Tet[tet * 4 + 1]] += vs;
V_sum[Tet[tet * 4 + 2]] += vs;
V_sum[Tet[tet * 4 + 3]] += vs;
}
for (int i = 0; i < number; i++)
{
V[i] = V_sum[i] / V_num[i];
}
Un = Mathf.Max(0.0f, Un - 0.005f);
}
// Update is called once per frame
void Update()
{
for (int l = 0; l < 10; l++)
_Update();
// Dump the vertex array for rendering.
Vector3[] vertices = new Vector3[tet_number * 12];
int vertex_number = 0;
for (int tet = 0; tet < tet_number; tet++)
{
vertices[vertex_number++] = X[Tet[tet * 4 + 0]];
vertices[vertex_number++] = X[Tet[tet * 4 + 2]];
vertices[vertex_number++] = X[Tet[tet * 4 + 1]];
vertices[vertex_number++] = X[Tet[tet * 4 + 0]];
vertices[vertex_number++] = X[Tet[tet * 4 + 3]];
vertices[vertex_number++] = X[Tet[tet * 4 + 2]];
vertices[vertex_number++] = X[Tet[tet * 4 + 0]];
vertices[vertex_number++] = X[Tet[tet * 4 + 1]];
vertices[vertex_number++] = X[Tet[tet * 4 + 3]];
vertices[vertex_number++] = X[Tet[tet * 4 + 1]];
vertices[vertex_number++] = X[Tet[tet * 4 + 2]];
vertices[vertex_number++] = X[Tet[tet * 4 + 3]];
}
Mesh mesh = GetComponent<MeshFilter>().mesh;
mesh.vertices = vertices;
mesh.RecalculateNormals();
}
}
image

参考链接
https://zhuanlan.zhihu.com/p/447263178
https://github.com/Teafox-Yang/GAMES103_HW_TEAFOX
https://www.bilibili.com/read/cv14754926
GAMES103 FEM 有限元模拟弹性房子的更多相关文章
- Java设计模式--模板方法模式
定义: 模板模式是一种行为设计模式,使用了JAVA的继承机制,在抽象类中定义一个模板方法,该方法引用了若干个抽象方法(由子类实现)或具体方法(子类可以覆盖重写).它的实现思路是,创建一个桩方法,并且定 ...
- 实现了一个简单的cage变形器
今天实现了一个简单变形器,可以用一个网格的形状影响另一个网格的形状. 如图,蓝色网格的形状被灰色网格操控. 当前的算法非常简单,就是计算蓝色网格每个点到灰色网格每个点的距离,以距离x次方的倒数作为权重 ...
- 考虑与Maya结合
今天改进了Hessian各块的计算代码,减少了一些内存操作.下一步准备把模拟平台与Maya结合,这样就可以利用Maya丰富的变形算法了. 这一步需要考虑以下问题: 1.把场景设置为某一帧.这一点可以用 ...
- 并行编程之CountdownEvent的用法
教程:http://blog.gkarch.com/threading/part5.html#the-parallel-class http://www.cnblogs.com/huangxinche ...
- [C#]『CountdownEvent』任务并行库使用小计
System.Threading.CountdownEvent 是一个同步基元,它在收到一定次数的信号之后,将会解除对其等待线程的锁定. CountdownEvent 专门用于以下情况:您必须使用 ...
- .Net并行编程之同步机制
一:Barrier(屏障同步) 二:spinLock(自旋锁) 信号量 一:CountdownEvent 虽然通过Task.WaitAll()方法也可以达到线程同步的目的. 但是Countdown ...
- D3、EChart、HighChart绘图demol
1.echarts: <!DOCTYPE html> <html> <head> <meta charset="utf-8" ...
- 西南交通大学结构服役安全及力学基础创新团队在Wiley出版英文专著(转载)
近日,西南交通大学力学与工程学院康国政教授与阚前华副教授受邀由John Wiley & Sons Ltd公司出版了英文专著 “Cyclic plasticity of Engineering ...
- 软件项目技术点(1)——d3.interpolateZoom-在两个点之间平滑地缩放平移
AxeSlide软件项目梳理 canvas绘图系列知识点整理 软件参考d3的知识点 我们在软件中主要用到d3.js的核心函数d3.interpolateZoom - 在两个点之间平滑地缩放平移.请 ...
- D3js-API介绍【中】
JavaScript可视化图表库D3.js API中文參考,d3.jsapi D3 库所提供的全部 API 都在 d3 命名空间下.d3 库使用语义版本号命名法(semantic versioning ...
随机推荐
- java基础之函数式接口
一.函数式接口在Java中是指:有且仅有一个抽象方法的接口,所以函数式接口就是可以适用于Lambda使用的接口 二.自定义函数式接口 格式: @FunctionalInterface //该注解可省, ...
- oracle的order by 中文排序原理
近期发现oracle的order by中文排序并不是完全按照拼音排序的 经过测试发现oracle的order by中文排序是按照中文的ASCII码排序的 查询字符ASCII码 select ascii ...
- eolinker流程用例步骤之脚本代码[Javascript]:读取多组数据,循环执行同一操作
特别注意:需要使用全局变量或者预处理前务必阅读本链接https://www.cnblogs.com/becks/p/13713278.html 场景(一)描述: 在未知有多少会员卡的前提下,对会员卡进 ...
- Salt之Cpu 100%无响应故障 Salt request timed out. The master is not responding
报错信息如下: Salt request timed out. The master is not responding. You may need to run your command with ...
- Web前端杂乱知识复习
OSI OSI是Open System Interconnect的缩写,意为开放式系统互联.其各个层次的划分遵循下列原则: (1)同一层中的各网络节点都有相同的层次结构,具有同样的功能. (2 ...
- xl2411p 显示器分辨率问题 IPS\TN
本来是想玩游戏来着,后来也没能玩起: 留下了个显示器明基xl2411p,昨天扒出来用起来吧. 玩游戏没毛病的,毕竟都是图片不存在文字的渲染问题,日常办公用起来就难受了,TN屏真是难受的了. 本来24寸 ...
- Java---switch...case中case可以匹配些什么
switch-case语句 case 标签可以是 : •类型为 char.byte.short 或 int 的常量表达式. •枚举常量. •从 Java SE 7 开始,case 标签还可以是字符串字 ...
- 项目开发管理最佳实践之一 --定义异常类exceptions
项目开发中,经常遇到需要抛出异常情况,可以根据项目存在情况定一个异常类,项目以django ,rest_framework为例 1 rom django.db.models.deletion impo ...
- golang 接口按需获取资源
场景 爬虫业务场景,我们需要调用三方接口获取代理ip地址,每个ip地址可以使用的时间有限和价格的,本着不浪费资源,我们在这里做一层封装. 当有其他业务调用我们接口的时候,会拉起定时任务,这个定时任务的 ...
- C# AggreateException
在 C# 中,AggregateException 是一种特殊类型的异常,它允许在多个异步任务中捕获并组合多个异常.当在一个异步任务中同时执行多个子任务时,如果其中任何一个子任务抛出了异常,那么父任务 ...
