OpenCV学习(18) 细化算法(6)
本章我们在学习一下基于索引表的细化算法。
假设要处理的图像为二值图,前景值为1,背景值为0。
索引表细化算法使用下面的8邻域表示法:

一个像素的8邻域,我们可以用8位二进制表示,比如下面的8邻域,表示为00111000=0x38=56
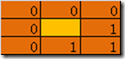
我们可以枚举出各种情况下,当前像素能否删除的表,该表大小为256。它的索引即为8邻域表示的值,表中存的值为0或1,0表示当前像素不能删除,1表示可以删除。deletemark[256]
比如下图第一个表示,索引值为0,它表示孤立点,不能删除,所以deletemark[0]=0,第二个表示索引值为17,它表示端点,也不能删除,所以deletemark[17]=0,第三个表示索引为21,删除的话会改变连通域数量,所以deletemark[21]=0,第四个表示索引值为96,此时可以删除,所以deletemark[96]=1。

最终我们会定义一张完整的表来表示当前像素能否删除。
索引表细化算法描述很简单。
1.找到轮廓,其值用4表示
2.查找值为4的轮廓,查找索引表判断能否删除,能删除的话把它置为0。
循环迭代1,2直到再也没有可以删除的点为止。
下面的算法的代码:
void gThin::cvidxThin1(cv::Mat& src, cv::Mat& dst)
{ if(src.type()!=CV_8UC1)
{
printf("只能处理二值或灰度图像\n");
return;
}
//非原地操作时候,copy src到dst
if(dst.data!=src.data)
{
src.copyTo(dst);
} // P0 P1 P2
// P7 P3
// P6 P5 P4
unsigned char deletemark[256] = {
0,0,0,0,0,0,0,1, 0,0,1,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
1,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,1,0,0,1,1,
1,1,0,1,0,0,0,1, 0,0,0,0,0,0,0,0,
1,1,0,1,0,0,0,1, 1,1,0,0,1,0,0,0,
0,1,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0
};//索引
int i, j;
int width, height;
//之所以减1,是方便处理8邻域,防止越界
width = src.cols -1;
height = src.rows -1;
int step = src.step;
int p0, p1, p2,p3,p4,p5,p6,p7;
uchar* img;
bool ifEnd;
bool border = false; //交换删除的次序,防止从一边细化
while(1)
{ border = !border;
img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j++)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]==0) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; //如果sum等于0,则不是内部点,是轮廓点,设置其像素值为2
int sum;
sum = p0 & p1 & p2 & p3 & p4 & p5 & p6 & p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(sum==0)
{
dst.at<uchar>(i,j) = 4; //满足删除条件,设置当前像素为0
} }
}
//printf("\n");
//PrintMat(dst);
//执行删除操作
ifEnd = false; img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j++)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} //printf("\n");
//PrintMat(dst);
//printf("\n"); //已经没有可以细化的像素了,则退出迭代
if(!ifEnd) break;
}
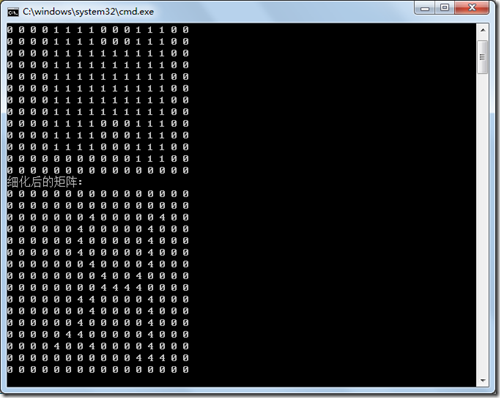
上面的算法可以看到细化后的轮廓偏右了,我们可以更改删除的循环条件,把循环拆分成三个,修改后的代码如下:
void gThin::cvidxThin(cv::Mat& src, cv::Mat& dst)
{ if(src.type()!=CV_8UC1)
{
printf("只能处理二值或灰度图像\n");
return;
}
//非原地操作时候,copy src到dst
if(dst.data!=src.data)
{
src.copyTo(dst);
} // P0 P1 P2
// P7 P3
// P6 P5 P4
unsigned char deletemark[256] = {
0,0,0,0,0,0,0,1, 0,0,1,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
0,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0, 1,0,0,0,1,0,1,1,
1,0,0,0,0,0,0,0, 1,0,1,1,1,0,1,1,
0,0,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,1,0,0,1,1,
1,1,0,1,0,0,0,1, 0,0,0,0,0,0,0,0,
1,1,0,1,0,0,0,1, 1,1,0,0,1,0,0,0,
0,1,1,1,0,0,1,1, 0,0,0,1,0,0,1,1,
0,0,0,0,0,0,0,0, 0,0,0,0,0,1,1,1,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0,
1,1,1,1,0,0,1,1, 1,1,0,0,1,1,0,0
};//索引
int i, j;
int width, height;
//之所以减1,是方便处理8邻域,防止越界
width = src.cols -1;
height = src.rows -1;
int step = src.step;
int p0, p1, p2,p3,p4,p5,p6,p7;
uchar* img;
bool ifEnd;
bool border = false; //交换删除的次序,防止从一边细化
while(1)
{ border = !border;
img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j++)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]==0) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; //如果sum等于0,则不是内部点,是轮廓点,设置其像素值为2
int sum;
sum = p0 & p1 & p2 & p3 & p4 & p5 & p6 & p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(sum==0)
{
dst.at<uchar>(i,j) = 4; //满足删除条件,设置当前像素为0
} }
}
//printf("\n");
//PrintMat(dst);
//执行删除操作
ifEnd = false; img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =1; j<width; j+=3)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =2; j<width; j+=3)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} img = dst.data;
for(i = 1; i < height; i++)
{
img += step;
for(j =3; j<width; j+=3)
{
uchar* p = img + j;
//如果p点是背景点,继续循环
if(p[0]!=4) continue;
p0 = p[-step-1]>0?1:0;
p1 = p[-step]>0?1:0;
p2 = p[-step+1]>0?1:0;
p3 = p[1]>0?1:0;
p4 = p[step+1]>0?1:0;
p5 = p[step]>0?1:0;
p6 = p[step-1]>0?1:0;
p7 = p[-1]>0?1:0; p1 = p1<<1;
p2 = p2<<2;
p3 = p3 <<3;
p4 = p4<<4;
p5 = p5<<5;
p6 = p6 <<6;
p7 = p7 << 7; //求的8邻域在索引表中的索引
int sum;
sum = p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7; //判断是否是邻接点或孤立点,0,1分别对于那个孤立点和端点
if(deletemark[sum] == 1)
{
dst.at<uchar>(i,j) = 0; //满足删除条件,设置当前像素为0
ifEnd = true;
} }
} //printf("\n");
//PrintMat(dst);
//printf("\n"); //已经没有可以细化的像素了,则退出迭代
if(!ifEnd) break;
} }
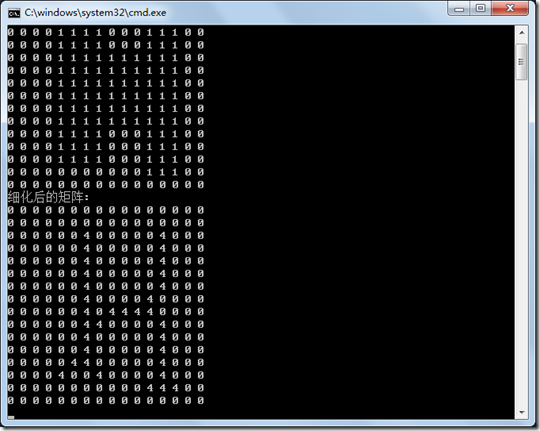
修改后的结果:
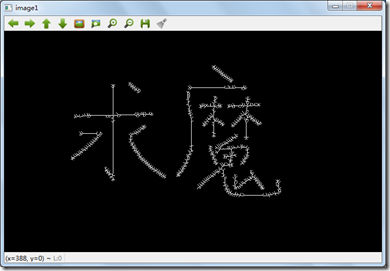
程序源代码:工程FirstOpenCV11
OpenCV学习(18) 细化算法(6)的更多相关文章
- OpenCV学习(16) 细化算法(4)
本章我们学习Rosenfeld细化算法,参考资料:http://yunpan.cn/QGRjHbkLBzCrn 在开始学习算法之前,我们先看下连通分量,以及4连通性,8连通性的概念: http://w ...
- OpenCV学习(15) 细化算法(3)
本章我们学习一下Hilditch算法的基本原理,从网上找资料的时候,竟然发现两个有很大差别的算法描述,而且都叫Hilditch算法.不知道那一个才是正宗的,两个算法实现的效果接近,第一种算 ...
- OpenCV学习(17) 细化算法(5)
本章我们看下Pavlidis细化算法,参考资料http://www.imageprocessingplace.com/downloads_V3/root_downloads/tutorials/con ...
- OpenCV学习(14) 细化算法(2)
前面一篇教程中,我们实现了Zhang的快速并行细化算法,从算法原理上,我们可以知道,算法是基于像素8邻域的形状来决定是否删除当前像素.还有很多与此算法相似的细化算法,只是判断的条件不一样. ...
- OpenCV学习(13) 细化算法(1)
程序编码参考经典的细化或者骨架算法文章: T. Y. Zhang and C. Y. Suen, "A fast parallel algorithm for thinning digita ...
- OpenCV学习(19) 细化算法(7)
最后再来看一种通过形态学腐蚀和开操作得到骨架的方法.http://felix.abecassis.me/2011/09/opencv-morphological-skeleton/ 代码非常简单: v ...
- c++opencv中线条细化算法
要达到的效果就是将线条尽量细化成单像素,按照论文上的Hilditch算法试了一下,发现效果不好,于是自己尝试着写了一下细化的算法,基本原理就是从上下左右四个方向向内收缩. 1.先是根据图片中的原则确定 ...
- OpenCV学习(9) 分水岭算法(3)
本教程我学习一下opencv中分水岭算法的具体实现方式. 原始图像和Mark图像,它们的大小都是32*32,分水岭算法的结果是得到两个连通域的轮廓图. 原始图像:(原始图像必须是3通道图像) Mark ...
- OpenCV学习(21) Grabcut算法详解
grab cut算法是graph cut算法的改进.在理解grab cut算之前,应该学习一下graph cut算法的概念及实现方式. 我搜集了一些graph cut资料:http://yunpan. ...
随机推荐
- Hadoop基准测试
其实就是从网络上copy的吧,在这里做一下记录 这个是看一下有哪些测试方式: hadoop jar /opt/cloudera/parcels/CDH-5.3.6-1.cdh5.3.6.p0.11/ ...
- console在ie下不兼容的问题(console在ie9下阻碍页面的加载,打开页面一片空白)
在页面中加入以下代码: window.console = window.console || (function() { var c = {}; c.log = c.warn = c.debug = ...
- hdu-1540线段树刷题
title: hdu-1540线段树刷题 date: 2018-10-18 19:55:21 tags: acm 刷题 categories: ACM-线段树 概述 哇,,,这道线段树的题可以说是到目 ...
- kali下利用weeman进行网页钓鱼
工具下载链接:https://files.cnblogs.com/files/wh4am1/weeman-master.zip 利用wget命令下载zip压缩包 利用unzip命令解压 接着直接cd进 ...
- 构造Huffman以及实现
构造Huffman 题目 在作业本上分别针对权值集合W=(6,5,3,4,60,18,77)和W=(7,2,4,5,8)构造哈夫曼树,提交构造过程的照片 错误回答 错误原因:遵循左边小于根右边大于根的 ...
- MySQL的五种日期和时间类型
MySQl中有多种表示日期和时间的数据类型.其中YEAR表示年份,DATE表示日期,TIME表示时间,DATETIME和TIMESTAMP表示日期和实践.它们的对比如下:YEAR ,字节数 ...
- hierarchyid有关的一些函数
于hierarchyid有关的一些函数主要有: GetAncestor :取得某一个级别的祖先 GetDescendant :取得某一个级别的子代 GetLevel :取得级别 ...
- 华为S5300系列交换机V200R001SPH027升级补丁
S5300SI-V200R001SPH027.pat 附件: 链接:https://pan.baidu.com/s/1ulE0j5Rp4xMkAaOjNGKLMA 密码:d5ze
- OpenVPN原理及实践文章收集(转)
一.基本理论篇 vpn原理及实现--一般理论 vpn原理及实现--隧道的一种实现 vpn原理及实现--虚拟网卡构建vpn vpn原理及实现--tcp还是udp Linux平台VPN技术概论 Linux ...
- 74HC125 74HCT125 74LV125 74LVC125
74HC125; 74HCT125Quad buffer/line driver; 3-state The 74HC125; 74HCT125 is a quad buffer/line driver ...
