栈式自动编码器(Stacked AutoEncoder)

起源：自动编码器

单自动编码器，充其量也就是个强化补丁版PCA，只用一次好不过瘾。

于是Bengio等人在2007年的 Greedy Layer-Wise Training of Deep Networks 中，

仿照stacked RBM构成的DBN，提出Stacked AutoEncoder，为非监督学习在深度网络的应用又添了猛将。

这里就不得不提 “逐层初始化”（Layer-wise Pre-training），目的是通过逐层非监督学习的预训练，

来初始化深度网络的参数，替代传统的随机小值方法。预训练完毕后，利用训练参数，再进行监督学习训练。

Part I 原理

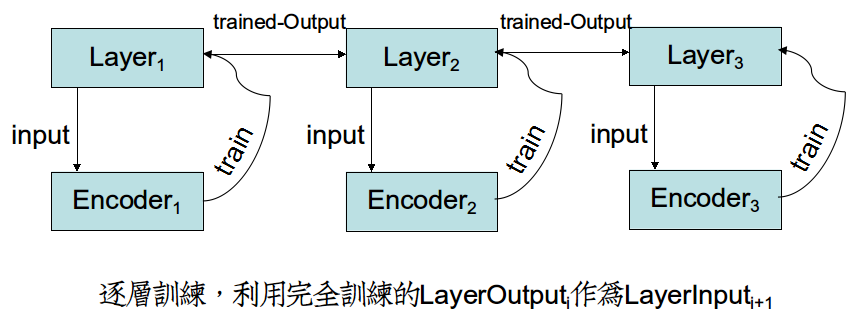
非监督学习网络训练方式和监督学习网络的方式是相反的。

在监督学习网络当中，各个Layer的参数W受制于输出层的误差函数，因而Layer_i参数的梯度依赖于Layer_i+1的梯度，形成了"一次迭代-更新全网络"反向传播。

但是在非监督学习中，各个Encoder的参数W只受制于当前层的输入，因而可以训练完Encoder_i，把参数转给Layer_{_i}，利用优势参数传播到Layer_i+1，再开始训练。

形成"全部迭代-更新单层"的新训练方式。这样，Layer_i+1效益非常高，因为它吸收的是Layer_i完全训练奉献出的精华Input。

Part II 代码与实现

主要参考 http://deeplearning.net/tutorial/SdA.html

栈式机在构造函数中，构造出各个Layer、Encoder，并且存起来。

Theano在构建栈式机中，易错点是Encoder、Layer的参数转移。

我们知道，Python的列表有深浅拷贝一说。Theano所有被shared标记的变量都是浅拷贝。

因而首先有这样的错误写法：

def __init__(self,rng,input,n_in,n_out,layerSize):

      ......

      for i in xrange(len(layerSize)):

            ......

            da.W=hidenlayer.W

            da.bout=hidenlayer.b

然后你在外部为da做grad求梯度的时候就报错了，提示说params和cost函数不符合。

这是因为cost函数的Tensor表达式在写cost函数时就确定了，这时候da这个对象刚好构造完，因而Tensor表达式中的da.W是构造随机值。

然后我们在da构造完了之后，手贱把da.W指向的内存改变了（浅拷贝相当于引用），这样算出的grad根本就不对。

其实这样写反了，又改成了这样

def __init__(self,rng,input,n_in,n_out,layerSize):

      ......

      for i in xrange(len(layerSize)):

            ......

            hidenlayer.W=da.W

            hidenlayer.b=da.bout

好吧，这样不会报错了，而且每训练一个Encoder，用get_value查看Layer的值确实改变了。但是，训练Encoder_i+1的时候，怎么感觉没效果？

其实是真的没效果，因为Layer_i的参数根本没有传播到Layer_i+1去。

Theano采用Python、C双内存区设计，在C代码中训练完Encoder_i时，参数并没有转到Layer_i中。但是我们明明建立了浅拷贝啊？

原来updates函数在C内存区中，根本没有觉察到浅拷贝关系，因为它在Python内存区中。

正确做法是像教程这样，在da构造时建立浅拷贝关系，当编译成C代码之后，所有Python对象要在C内存区重新构造，自然就在C内存区触发了浅拷贝。

 da=dA(rng,layerInput,InputSize,self.layerSize[i],hidenlayer.W,hidenlayer.b)

或者训练完Encoder_i，强制把Encoder_i参数注入到C内存区的Layer_i里。

updateModel=function(inputs=[],outputs=[],updates=[(....)]，

updateModel()

Theano的写法风格近似于函数式语言，对象、函数中全是数学模型。一旦构造完了之后，就无法显式赋值。

所以，在Python非构造函数里为对象赋值是愚蠢的，效果仅限于Python内存区。但是大部分计算都在C内存区，所以需要updates手动把值打进C内存区。

updates是沟通两区的桥梁，一旦发现Python内存区中有建立浅拷贝关系，就会把C内存区中值更新到Python内存区。（有利于Python中保存参数）

但是绝对不会自动把Python内存区值，更新到C内存区当中。（这点必须小心）

这种做法可以扩展到，监督训练完之后，参数的保存与导入。