Z字形扫描矩阵

问题描述
　　在图像编码的算法中，需要将一个给定的方形矩阵进行Z字形扫描(Zigzag Scan)。给定一个n×n的矩阵，Z字形扫描的过程如下图所示：

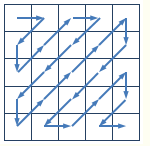
　　对于下面的4×4的矩阵，
　　1 5 3 9
　　3 7 5 6
　　9 4 6 4
　　7 3 1 3
　　对其进行Z字形扫描后得到长度为16的序列：
　　1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3
　　请实现一个Z字形扫描的程序，给定一个n×n的矩阵，输出对这个矩阵进行Z字形扫描的结果。
输入格式
　　输入的第一行包含一个整数n，表示矩阵的大小。
　　输入的第二行到第n+1行每行包含n个正整数，由空格分隔，表示给定的矩阵。
输出格式
　　输出一行，包含n×n个整数，由空格分隔，表示输入的矩阵经过Z字形扫描后的结果。
样例输入
4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3
样例输出
1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3
评测用例规模与约定
　　1≤n≤500，矩阵元素为不超过1000的正整数。

---

分析这类题，首先要找出扫描的规律，从题目中可以发现，扫描是成Z字形的。那么也就是说对于扫描输出有四种状态，每次输出要判定下一次的行走路线，走一步就输出一个。

四种状态为{right,leftDown,down,rightUp}。

开始我还怀疑，Z字形扫描矩阵是否能够遍历矩阵所有的元素。下面我们来分析一下：

1、前提是这个矩阵是一个n维方阵，假设为A_nxn.

2、从输出当前的元素A[i][j]，并根据当前的状态来判断下一步的扫描状态。该如何判断呢？可以发现每次在执行完当前状态后，行号i或者列号j都有可能发生改变，那么就可以结合当前状态和行，列号的取值来判定下一步的行走路线。

从上图中我们可以发现：

right状态始终在首行或者尾行上执行，并且执行right状态后列号j会增加1，即j = j+1。所以我们可以根据当前状态的下一步状态有两种：

当i == 0时，state = leftDown;

当i == n-1时，state = rightUp。

执行完leftDown状态后，i = i+1,j = j-1，其下一步状态有三种：

当 j == 0 && i != n-1时，state = down;

当 row == n-1时，state = right;

其它情况，state = leftDown（自身状态）。

对于rightUp和down状态，其分析方法和上面两种类似，就不再做分析。

综合上面分析来看，状态每次要发生改变的话，行号或者列号必须处于临界状态，即它们的取值为{0,n-1}。

---

给出代码：

#include <iostream>

using namespace std;

int A[][];
enum  Choice
{
    rightTowards,//向移动
    rightUp,//向右上移动
    down,//向下移动
    leftDown//向左下移动
};

void zigzagScan(int n)
{
    for (int i = ; i < n; ++i)
    for (int j = ; j < n; ++j)
        cin >> A[i][j];
    int row = , col = ;
    Choice choice = rightTowards;
    //row = n-1&&col = n-1的情况在while循环结束后处理，防止出现越界的情况
    while (row != n -  || col != n - )
    {
        cout << A[row][col] << ' ';
        switch (choice)
        {
        case rightTowards:
            col++;
            if (row == )
                choice = leftDown;
            else
                choice = rightUp;
            break;
        case rightUp:
            row--;
            col++;
            if (row ==  && col != n - )
                choice = rightTowards;
            else if (col == n - )
                choice = down;
            else
                choice = rightUp;
            break;
        case down:
            row++;
            if (col == )
                choice = rightUp;
            else
                choice = leftDown;
            break;
        case leftDown:
            row++;
            col--;
            if (col ==  && row != n - )
                choice = down;
            else if (row == n - )
                choice = rightTowards;
            else
                choice = leftDown;
            break;
        }
    }
    cout << A[n - ][n - ];
}

void main(void)
{
    int n;
    while (cin >> n)
    {
        zigzagScan(n);
    }
}