AMQ(approximate membership queries)介绍

目录

• 简介
• 举例
  • Bloom Filter
  • 算法过程
    • 1）位数组：
    • 2）添加元素，k个独立hash函数
    • 3）判断元素是否存在集合
  • Quotient Filter and Cascade Filter
• 参考文献

简介

AMQ(approximate membership queries近似成员查询):

• 是一种字典数据结构
• 是在空间使用和查询错误率的权衡
• 用于解决大量数据的处理
• 拥有以下操作
  • 查找
  • 插入
  • 可选择元素的删除
• 设e误检率，当查询时报出absent值时，e的概率为误检，1-e的概率为确实没有该元素。
• 可以通过调整e值来调整准确度和空间使用的关系

举例

Bloom Filter

Bloom filter

• Bloom Filter（BF）是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合
• 历史：Bloom-Filter，即布隆过滤器，1970年由Bloom中提出。
• 应用：用于检索一个元素是否在一个集合中。
• 特点：Bloom Filter有可能会出现错误判断，但不会漏掉判断。
• 适用场景：Bloom Filter”不适合那些“零错误的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter比其他常见的算法（如hash，折半查找）极大节省了空间。
• 优点：是空间效率和查询时间都远远超过一般的算法，
• 缺点：是有一定的误识别率和删除困难。

算法过程

• 原理要点：一是位数组， 二是k个独立hash函数。

1）位数组：

• 
• 假设Bloom Filter使用一个m比特的数组来保存信息，初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0，即BF整个数组的元素都设置为0。

2）添加元素，k个独立hash函数

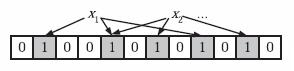
• 为了表达S={x1, x2,…,xn}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。

• 当我们往Bloom Filter中增加任意一个元素x时候，我们使用k个哈希函数得到k个哈希值，然后将数组中对应的比特位设置为1。即第i个哈希函数映射的位置hashi(x)就会被置为1（1≤i≤k）。

• 注意，如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位，即第二个“1“处）。

3）判断元素是否存在集合

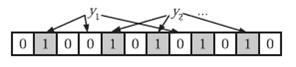
• 在判断y是否属于这个集合时，我们只需要对y使用k个哈希函数得到k个哈希值，如果所有hashi(y)的位置都是1（1≤i≤k），即k个位置都被设置为1了，那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y1就不是集合中的元素（因为y1有一处指向了“0”位）。y2或者属于这个集合，或者刚好是一个false positive。

• 显然这个判断并不保证查找的结果是100%正确的。

• 更多详细信息

Quotient Filter and Cascade Filter

• Quitient Filter 和Cascade Filter算法由Bender等人设计，是一个空间效率高的概率性数据结构
• 应用：用于检索一个元素是否在一个集合中。
• 优点：对插入、查询、删除操作由高吞吐量，比Bloom Filter高了两个数量级。
• 更多详情见[3][4]

参考文献

[1] https://www.cnblogs.com/zhxshseu/p/5289871.html
[2] https://en.wikipedia.org/wiki/Bloom_filter
[3] https://en.wikipedia.org/wiki/Quotient_filter
[4] Don’t Thrash: How to Cache your Hash on Flash