几何+线段交点+spfa（POJ1066）

Treasure Hunt

Time Limit : 2000/1000ms (Java/Other)   Memory Limit : 20000/10000K (Java/Other)

Total Submission(s) : 3   Accepted Submission(s) : 2

Problem Description

Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline
walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want
to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For
structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors. 

An example is shown below: 

 

Input

The input will consist of one case. The first line will be an integer n (0 <= n <= 30) specifying number of interior walls, followed by n lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4 enclosing walls of the pyramid have fixed endpoints
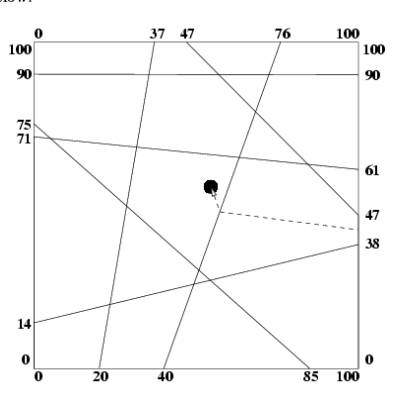
at (0,0); (0,100); (100,100) and (100,0) and are not included in the list of walls. The interior walls always span from one exterior wall to another exterior wall and are arranged such that no more than two walls intersect at any point. You may assume that
no two given walls coincide. After the listing of the interior walls there will be one final line containing the floating point coordinates of the treasure in the treasure room (guaranteed not to lie on a wall).

 

Output

Print a single line listing the minimum number of doors which need to be created, in the format shown below.

 

Sample Input

7
20 0 37 100
40 0 76 100
85 0 0 75
100 90 0 90
0 71 100 61
0 14 100 38
100 47 47 100
54.5 55.4 

 

Sample Output

Number of doors = 2 

 题意：给出一个0,0,100,100的正方形，然后给出n条线段，线段的两个端点一定在该正方形的边界上，且最多有两个线段交于一点，形成的图中则被分割成多个单元线段，每个单元线段的中点有一扇门，然后其他就是墙，然后给出宝藏的坐标，问从外界进入宝藏的位置至少需要经过多少门？

分析：首先对每条初始线段枚举，包括正方形的边界，求分割后的单元线段存在L中，然后对于每个线段把中点即门的坐标存在p中，记住把宝藏的位置存入p中，然后两两枚举p坐标构成的线段，如果中间没有其他L挡住，则可以连通ij，设权值是1，然后用spfa求出以宝藏为起点的单源最短路，从到达边界的门中取得最小值就是答案：

#include"string.h"
#include"stdio.h"
#include"iostream"
#include"algorithm"
#include"queue"
#include"stack"
#define M 1000
#define N 100009
#include"stdlib.h"
#include"math.h"
#define inf 10000000000000000LL
#define INF 0x3f3f3f3f
const double PI=acos(-1.0);
#define eps 1e-10
using namespace std;
struct st
{
    int u,v,next;
    st(int vv)
    {
        v=vv;
    }
};
vector<st>edge[M];
int use[M],dist[M];
void spfa(int s,int n)
{
    int i;
    for(i=1;i<=n;i++)
    {
        dist[i]=INF;
        use[i]=0;
    }
    queue<int>q;
    dist[s]=0;
    use[s]=1;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(i=0;i<(int)edge[u].size();i++)
        {
            int v=edge[u][i].v;
            if(dist[v]>dist[u]+1)
            {
                dist[v]=dist[u]+1;
                if(!use[v])
                {
                    use[v]=1;
                    q.push(v);
                }
            }
        }
    }
}
struct node
{
    double x,y;
    int id;
    node (){}
    node (double xx,double yy):x(xx),y(yy){}
    node operator -(node p)
    {
        return node (x-p.x,y-p.y);
    }
    double operator *(node p)
    {
        return x*p.y-y*p.x;
    }
    double operator ^(node p)
    {
        return x*p.x+y*p.y;
    }
}p[M];
struct line
{
    node s,e;
    int id;
    line(){}
    line(double x1,double y1,double x2,double y2)
    {
        s.x=x1;
        s.y=y1;
        e.x=x2;
        e.y=y2;
    }
    line(node a,node b)
    {
        s=a;
        e=b;
    }
}l[M],L[M];
double max(double a,double b)
{
    return a>b?a:b;
}
double min(double a,double b)
{
    return a<b?a:b;
}
double cross(node a,node b,node c)
{
    return (b-a)*(c-a);
}
double dot(node a,node b,node c)
{
    return (b-a)^(c-a);
}
double len(node a)
{
    return sqrt(a^a);
}
double dis(node a,node b)
{
    return len(b-a);
}
int judge(line a,line b)
{
    if(fabs(cross(a.s,a.e,b.s))<eps&&fabs(cross(a.s,a.e,b.e))<eps)//重合
        return 1;
    else if(fabs((a.e-a.s)*(b.e-b.s))<eps)//平行
        return -1;
    else
        return 0;//相交
}
node intersection(line a,line b)
{
    double a1=a.s.y-a.e.y;
    double b1=a.e.x-a.s.x;
    double c1=(a.e.y-a.s.y)*a.s.x+a.s.y*(a.s.x-a.e.x);
    double a2=b.s.y-b.e.y;
    double b2=b.e.x-b.s.x;
    double c2=(b.e.y-b.s.y)*b.s.x+b.s.y*(b.s.x-b.e.x);
    node ret;
    ret.x=(c2*b1-c1*b2)/(a1*b2-a2*b1);
    ret.y=(c2*a1-c1*a2)/(a2*b1-a1*b2);
    return ret;
}
int paichi(line a,line b)//快速排斥，若通过快速排斥进行跨立实验，否则无交点；
{
    if(max(a.e.x,a.s.x)>=min(b.s.x,b.e.x)
       &&max(b.s.x,b.e.x)>=min(a.s.x,a.e.x)
       &&max(a.s.y,a.e.y)>=min(b.s.y,b.e.y)
       &&max(b.s.y,b.e.y)>=min(a.s.y,a.e.y))
        return 1;
    else
        return 0;
}
int kuali(line a,line b)//跨立实验（通过相互跨立则可确定两线段相交返回1）
{
    if(cross(a.s,a.e,b.s)*cross(a.s,a.e,b.e)<=0
       &&cross(b.s,b.e,a.s)*cross(b.s,b.e,a.e)<=0)
        return 1;
    return 0;
}
int cmp(node a,node b)
{
    if(fabs(a.x-b.x)<eps)
        return a.y<b.y;
    else
        return a.x<b.x;
}
int main()
{
    int n,i,j,k;
    while(scanf("%d",&n)!=-1)
    {
        for(i=1;i<=n;i++)
        scanf("%lf%lf%lf%lf",&l[i].s.x,&l[i].s.y,&l[i].e.x,&l[i].e.y);
        l[++n]=line(0,0,100,0);
        l[++n]=line(100,0,100,100);
        l[++n]=line(100,100,0,100);
        l[++n]=line(0,100,0,0);
        node tar;
        scanf("%lf%lf",&tar.x,&tar.y);
        int num=0;
        for(i=1;i<=n;i++)
        {
            k=0;
            p[k++]=node(l[i].s);
            p[k++]=node(l[i].e);
            for(j=1;j<=n;j++)
            {
                if(i==j)continue;
                if(paichi(l[i],l[j])&&kuali(l[i],l[j]))
                {
                    p[k++]=intersection(l[i],l[j]);
                }
            }
            sort(p,p+k,cmp);
            for(j=1;j<k;j++)
            {
                L[++num]=line(p[j-1],p[j]);
                L[num].id=i;
            }
        }
        for(i=1;i<=num;i++)
        {
            p[i]=node((L[i].s.x+L[i].e.x)/2,(L[i].s.y+L[i].e.y)/2);
            p[i].id=L[i].id;
        }
        p[++num]=tar;
        p[num].id=-1;
        for(i=1;i<=num;i++)
        {
            for(j=i+1;j<=num;j++)
            {
                line PL=line(p[i],p[j]);
                int flag=0;
                for(k=1;k<=n;k++)
                {
                    if(p[i].id==k||p[j].id==k)continue;
                    if(paichi(PL,l[k])&&kuali(PL,l[k]))
                    {
                        flag=1;
                        break;
                    }
                }
                if(!flag)
                {
                    edge[i].push_back(j);
                    edge[j].push_back(i);
                }
            }
        }
        spfa(num,num);
        int ans=INF;
        for(i=1;i<=num;i++)
        {
            if(p[i].id>=n-3)
            {
                //printf("%d ",dist[i]);
                if(ans>dist[i])
                {
                    ans=dist[i];
                    k=i;
                }
            }
        }
        printf("Number of doors = %d\n",ans);
        //printf("%lf %lf\n",p[k].x,p[k].y);
        for(i=1;i<=num;i++)
            edge[i].clear();
    }
}