南京网络赛I-Skr【回文树模板】

• 19.32%
• 1000ms
• 256000K

A number is skr, if and only if it's unchanged after being reversed. For example, "12321", "11" and "1" are skr numbers, but "123", "221" are not. FYW has a string of numbers, each substring can present a number, he wants to know the sum of distinct skr number in the string. FYW are not good at math, so he asks you for help.

Input

The only line contains the string of numbers SS.

It is guaranteed that 1 \le S[i] \le 91≤S[i]≤9, the length of SS is less than 20000002000000.

Output

Print the answer modulo 10000000071000000007.

样例输入1复制

111111

样例输出1复制

123456

样例输入2复制

1121

样例输出2复制

135

题目来源

ACM-ICPC 2018 南京赛区网络预赛

就是一道回文自动机的模板

回文自动机用来求一个字符串中的种类或个数

因为这道题还去了解了一下Trie树和AC自动机 虽然好像还不是很会用 有空去找道题做一下好了

回文自动机的结构（我还是喜欢叫他自动机， 虽然我都不太理解自动机）：

存在两个树结构，分别记录奇数|偶数长度的回文；

每个点记录一种字符串（但是由于可以通过根到该节点的路径确定这个字符串是什么，于是并不需要真的在该节点记录/*写下*/这个信息）【Trie树】

每个节点连字符x边向一个子节点，表示在她的左右两边加x构成的回文是这个总字符串的子串（根节点相关部分单独定义）；

每个节点连一条fail指针向其最长后缀回文；

一开始回文树有两个节点，0表示偶数长度串的根和1表示奇数长度串的根，且len[0] = 0，len[1] = -1，last = 0，S[0] = -1

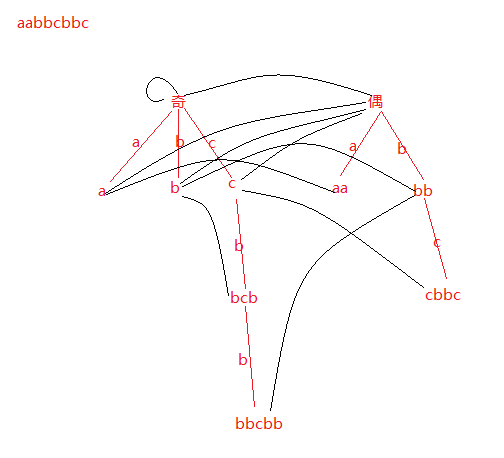偶数的fail指向奇数的

详细过程见：https://blog.csdn.net/u013368721/article/details/42100363

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#include<vector>
#include<set>
//#include<bits/stdc++.h>
#define inf 0x7f7f7f7f7f7f7f7f
using namespace std;
typedef long long LL;

const int maxn = 2e6 + 10;
const LL mod = 1000000007;

LL read()
{
    LL x = 0, f = 1;
    register char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-'){
            f = -1;
        }
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

LL pow_mod(LL a, LL b, LL p)
{
    LL ret = 1;
    while(b){
        if(b & 1){
            ret = (ret * a) % p;
        }
        a = (a * a) % p;
        b >>= 1;
    }
    return ret;
}

LL fermat(LL a, LL p)//求a关于b的逆元
{
    return pow_mod(a, p - 2, p);
}

LL ans, llen;
LL _10[maxn], inv10[maxn];
LL sum[maxn], rsum[maxn];//sum[i]是子串0-i表示的数值， rsum[i]是子串i到len表示的数值
char str[maxn];

struct PT{
    char s[maxn];//s[i]表示第i个添加的字符
    int last, cur, tot;//last指向新添加一个字母后所形成的最长回文串表示的节点, tot表示节点个数
    int son[maxn][10];
    int fail[maxn], len[maxn];//len[i]表示编号为i的节点表示的回文串的长度
    void init(){
        s[0] = -1;
        last = cur = 0;
        tot = 1;
        for(int i = 0; i <= 9; i++){
            son[0][i] = son[1][i] = 0;
        }
        len[0] = 0;
        len[1] = -1;
        fail[0] = 1;
        fail[1] = 0;
    }

    int node(int l){
        ++tot;
        for(int i = 0; i <= 9; i++){
            son[tot][i] = 0;
        }
        fail[tot] = 0;
        len[tot] = l;
        return tot;
    }

    int getfail(int x){
        while(s[cur - len[x] - 1] ^ s[cur]){
            x = fail[x];
        }
        return x;
    }

    void add(int pos){
        s[++cur] = str[pos];
        int t = getfail(last);
        int c = str[pos] - '0';
        if(son[t][c] == 0){//这个回文串没有出现过
            int o = node(len[t] + 2);
            fail[o] = son[getfail(fail[t])][c];
            son[t][c] = o;
            LL lo = ((sum[llen] - rsum[pos - (len[t] + 2) + 1]) % mod + mod) % mod;
            LL hi = rsum[pos + 1];
            LL all = lo + hi;
            if(all >= mod) all %= mod;
            LL t = ((sum[llen] - all) % mod + mod) % mod;
            if(t >= mod) t %= mod;
            if(llen - pos + 1 - 1 > 0) ans = ans + t * inv10[llen- pos + 1 - 1] % mod;
            else
                ans = ans + t;
            if(ans >= mod) ans %= mod;
        }
        last = son[t][c];
    }
}pt;

int main()
{
    _10[0] = 1;
    for(int i = 1; i <= maxn - 1; i++){
        _10[i] = _10[i - 1] * 10;
        if(_10[i] >= mod){
            _10[i] %= mod;
        }
        inv10[i] = fermat(_10[i], mod);
    }
    while(~scanf("%s", str + 1)){
        memset(sum, 0, sizeof(sum));
        memset(rsum, 0, sizeof(rsum));
        ans = 0;
        sum[0] = 0;
        pt.init();
        llen = strlen(str + 1);
        for(int i = 1; i <= llen; i++){
            sum[i] = sum[i - 1] * 10 + (int)(str[i] - '0');
            if(sum[i] >= mod) sum[i] %= mod;
        }
        rsum[llen + 1] = 0;
        for(int i = llen; i >= 1; i--){
            rsum[i] = rsum[i + 1] + (int)(str[i] - '0') * _10[llen - i] % mod;
            if(rsum[i] >= mod) rsum[i] %= mod;
        }
        ans = 0;
        for(int i = 1; i <= llen; i++){
            pt.add(i);
        }
        printf("%lld\n", (LL)ans % mod);
    }
	return 0;
}