降维（三）LLE与其他降维技术

LLE

局部线性嵌入，Locally Linear Embedding（LLE）是另一个功能强大的非线性降维（nonlinear dimensional reduction，NLDR）技术。它是一个流形学习技术，并不基于投影。简单地说，LLE工作的方式是：首先衡量每个训练实例与它最近的邻居们（closest neighbors，c.n.）的线性相关程度，然后在这些局部关系可以得到最好地保存的情况下，寻找一个低维的表示训练集的方式。这个方法在展开弯曲的流形时非常有用，特别是数据集中没有太多的噪点时。

下面的代码使用sk-learn的LocallyLinearEmbedding类将一个瑞士卷展开：

from sklearn.manifold import LocallyLinearEmbedding

lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_reduced = lle.fit_transform(X)

生成的2D数据集结果如下图所示：

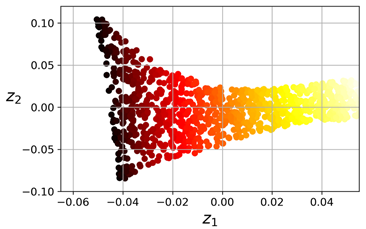
我们可以看到，瑞士卷被完全地展开了，并且实例之间的距离非常好地在局部保持了。不过，在更大的规模层面上，距离并没有保持好：左边部分的瑞士卷是伸展的，而右边的部分是紧缩的。尽管如此，LLE在流形建模中仍表现的非常好。

LLE的具体工作方式为：对于每条训练实例x⁽ⁱ⁾，算法识别它的k个最邻近邻居（在上面的代码中k=10），然后尝试用它的这些邻居以一个线性函数的方式重构x⁽ⁱ⁾。更具体地说，它会找到一组权重w_i,j使得x⁽ⁱ⁾与∑wi,jx(j)（其中j 初始为1，累加到第m）之间的平方距离尽可能的小，如果x^(j)并不是x⁽ⁱ⁾的最近k个邻居之一，则假设w_i,j = 0。所以LLE的第一步是下面的带约束优化问题，这里W是权重矩阵，包含所有的权重w_i,j。第二个约束是对每个训练实例x⁽ⁱ⁾的权重们一个简单的标准化约束：

在这个步骤完成后，权重矩阵Wˆ（包含权重wˆi,j）便对训练实例之间的局部线性关系进行了编码。第二个步骤就是将训练实例映射到一个d维的空间中（d < n），同时尽可能地保留这些局部关系。如果z⁽ⁱ⁾是x⁽ⁱ⁾在这个d维空间里的像（image），则我们会想要z⁽ⁱ⁾与∑wˆi,jz(j) （其中j初始为1，累加到第m）之间的平方距离尽可能的小。这个想法便产生了下一个带约束的优化问题（如下公式所示）。它与第一个步骤非常像，但是并不是固定实例然后找到最优的权重，而是做相反的事情：保持权重固定，在低维空间中找到实例的image的最优位置。需要主要的是，这里Z是包含了所有z⁽ⁱ⁾的矩阵。

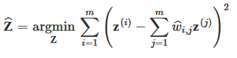
sk-learn的LLE实现，它的计算复杂度，找到k个最近邻居的复杂度是O(m log(m)n log(k))，优化权重的复杂度是O(mnk³)，以及构造低维空间表示的复杂度是O(dm²)。可惜的是，在最后一个公式中m²的会让这个算法对超大数据集的扩展十分糟糕。

其他降维技术

还有很多种其他的降维技术，其中部分有在sk-learn中提供，下面是最热门的几个：

• 随机投影
  • 如它名称所示，使用一个随机的线性投影，将数据投影到一个低维空间中。这个听起来很奇怪，不过结果证明，这种随机投影实际上几乎可以很好的保留距离。它的降维质量取决于数据的条目以及目标label的维度，而却不是初始的维度。可以查看sklearn.random_projection 包获取更多信息
• 多维缩放（Multidimensional Scaling，MDS）
  • 在尽量保持实例之间距离的情况下减少维度
• Isomap
  • 通过将每个实例与它的最近邻居连接起来，而创建一个图。然后在尽量保持实例之间测地距离（geodesic distances）的情况下减少维度
• t-分布式随机邻居嵌入（t-Distributed Stochastic Neighbor Embedding（t-SNE）
  • 在保持相似实例接近而非相似实例远离的情况下减少维度。它大部分用于数据可视化，特别是在可视化高维空间中的实例簇（clusters of instances）时（例如，将MNIST图片在2D上进行可视化）。
• 线性判别分析（Linear Discriminant Analysi，LDA）
  • 它是一个分类算法，不过在训练时，它会学习最能分辨不同类别的判别轴（discriminative axes），然后这些轴可以被用于定义一个超平面，数据之后便可以投影到这个超平面上。这个方法的好处是投影会保持不同类别尽可能的远离，所以LDA是一个很好的降维技术，它可以用于在执行另外的分类算法（如SVM）前进行降维。

下图展示了其中几种技术：