[洛谷P3959][NOIP2017提高组] 宝藏

[NOIP2017 提高组] 宝藏

题目描述

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了 \(n\) 个深埋在地下的宝藏屋， 也给出了这 \(n\) 个宝藏屋之间可供开发的 \(m\) 条道路和它们的长度。

小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远，也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏屋之间的道路无需再开发。

新开发一条道路的代价是 \(\mathrm{L} \times \mathrm{K}\)。其中 \(L\) 代表这条道路的长度，\(K\) 代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋） 。

请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代价最小，并输出这个最小值。

输入格式

第一行两个用空格分离的正整数 \(n,m\)，代表宝藏屋的个数和道路数。

接下来 \(m\) 行，每行三个用空格分离的正整数，分别是由一条道路连接的两个宝藏屋的编号（编号为 \(1-n\)），和这条道路的长度 \(v\)。

输出格式

一个正整数，表示最小的总代价。

样例 #1

样例输入 #1

4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1

样例输出 #1

4

样例 #2

样例输入 #2

4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 2

样例输出 #2

5

提示

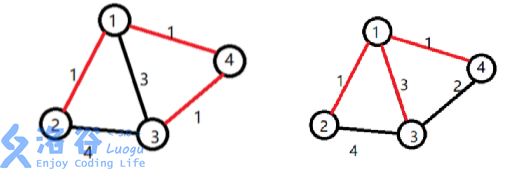
【样例解释 \(1\)】

小明选定让赞助商打通了 \(1\) 号宝藏屋。小明开发了道路 \(1 \to 2\)，挖掘了 \(2\) 号宝藏。开发了道路 \(1 \to 4\)，挖掘了 \(4\) 号宝藏。还开发了道路 \(4 \to 3\)，挖掘了 \(3\) 号宝藏。

工程总代价为 $1 \times 1 + 1 \times 1 + 1 \times 2 = 4 $。

【样例解释 \(2\)】

小明选定让赞助商打通了 \(1\) 号宝藏屋。小明开发了道路 \(1 \to 2\)，挖掘了 \(2\) 号宝藏。开发了道路 \(1 \to 3\)，挖掘了 \(3\) 号宝藏。还开发了道路 \(1 \to 4\)，挖掘了 \(4\) 号宝藏。

工程总代价为 \(1 \times 1 + 3 \times 1 + 1 \times 1 = 5\)。

【数据规模与约定】

对于 $ 20%$ 的数据： 保证输入是一棵树，\(1 \le n \le 8\)，\(v \le 5\times 10^3\) 且所有的 \(v\) 都相等。

对于 \(40\%\) 的数据： \(1 \le n \le 8\)，\(0 \le m \le 10^3\)，\(v \le 5\times 10^3\) 且所有的 \(v\) 都相等。

对于 $ 70%$ 的数据： \(1 \le n \le 8\)，\(0 \le m \le 10^3\)，\(v \le 5\times 10^3\)。

对于 $ 100%$ 的数据： \(1 \le n \le 12\)，\(0 \le m \le 10^3\)，\(v \le 5\times 10^5\)。

这个数据范围，一看就知道是状压 dp。同时肯定是一层一层dp的。

定义 \(dp_{i,s1,s2}\) 为现在层数为 \(i\)，已经开通了的点是 \(s1\)，最后一层是 \(s2\)，然后要枚举 \(s3\) 为下一层所连的点集合，转移。

但是这样复杂度会爆炸。发现其实 \(s2\) 不用记在 dp 范围内。因为当 \(s3\) 接到不是最近一层的点时，他的代价会更劣，本来没有 \(i\) 层被算成了 \(i\) 层。所以我们只要找出 \(s1\) 和 \(s3\) 的所有连接方式中最优的就行了。

\(s3\) 子集枚举，复杂度 \(O(n3^n)\)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=13;
int n,m,g[N][N];
LL ans=1e18,dp[1<<N][N];//dp[s][i]:
int main()
{
	memset(dp,0x7f,sizeof(dp));
	memset(g,0x7f,sizeof(g));
	scanf("%d%d",&n,&m);
	for(int i=1,u,v,w;i<=m;i++)
	{
		scanf("%d%d%d",&u,&v,&w),--u,--v;
		g[u][v]=g[v][u]=min(g[u][v],w);
	}
	for(int i=0;i<n;i++)
		dp[1<<i][1]=0;
	for(int i=1;i<(1<<n);i++)
	{
		for(int j=i&(i-1);j;j=(j-1)&i)
		{
//			printf("%d %d\n",i,j);
			int s=i^j,ret=0,fl=0;
			for(int a=0;a<n;a++)
			{
				if(j>>a&1)
				{
					int mn=1e6;
					for(int b=0;b<n;b++)
						if(s>>b&1&&g[a][b])
							mn=min(mn,g[a][b]);
					if(mn==1e6)
						fl=1,a=n;
					ret+=mn;
				}
			}
			if(fl)
				continue;
			for(int k=2;k<=n;k++)
				dp[i][k]=min(dp[i][k],dp[s][k-1]+ret*1LL*(k-1));
		}
	}
//	for(int i=1;i<(1<<n);i++)
//	{
//		for(int j=1;j<=n;j++)
//			printf("%d ",dp[i][j]);
//		puts("");
//	}
	for(int i=1;i<=n;i++)
		ans=min(ans,dp[(1<<n)-1][i]);
	printf("%lld",ans);
}