[转帖]LSM-Tree:从入门到放弃——入门：基本概念、操作和Trade-Off分析

https://zhuanlan.zhihu.com/p/428267241

LSM-Tree，全程为日志结构合并树，有趣的是，这个数据结构实际上重点在于日志结构合并，和 tree 本身的关系并不是特别大(除了各种可能的天外飞仙式的工程优化，一般来说只有 level0 采用了平衡树的结构)

LSM-Tree 通过“极端”的磁盘顺序写的方案，通常有极其离谱的写吞吐量，被大量应用于Cassandra、LevelDB、RocksDB、HBase等 NoSQL 数据库底层存储引擎中。

LSM-Tree 通常没有一种固定死的实现方式，更多的是一系列符合以下设计方法论的思想构成的实现：

1. 多个横跨内存和磁盘的树状数据结构构成的森林
2. 不同 level (一般来说也可以理解为新旧或冷热)数据分级，从 level-0 到 level-n ，一般只有 level-0 在内存中，其他的level通常落在磁盘上。
3. level-0 通常采用平衡的排序树、跳表或 TreeMap 等有序的数据结构，方便从内存顺序写到磁盘中。磁盘中的 level 本质是排序好后 appendonly 写到磁盘上的文件(也可以认为是中序遍历后的“树”)。
4. 定期归并，每层子树一般有一个阈值大小，达到阈值后会归并本 level 的块并到下一 level。
5. 通常只允许内存中的 level (一般特指 level-0 )原地更新，磁盘上不允许数据变更，而是选择采用 appendonly 的方式写日志。

符合以上定义的实现构成了一般意义上我们理解的 LSM-Tree。构成如下图的结构(图片来自知乎用户康乐为撰写的文章)：

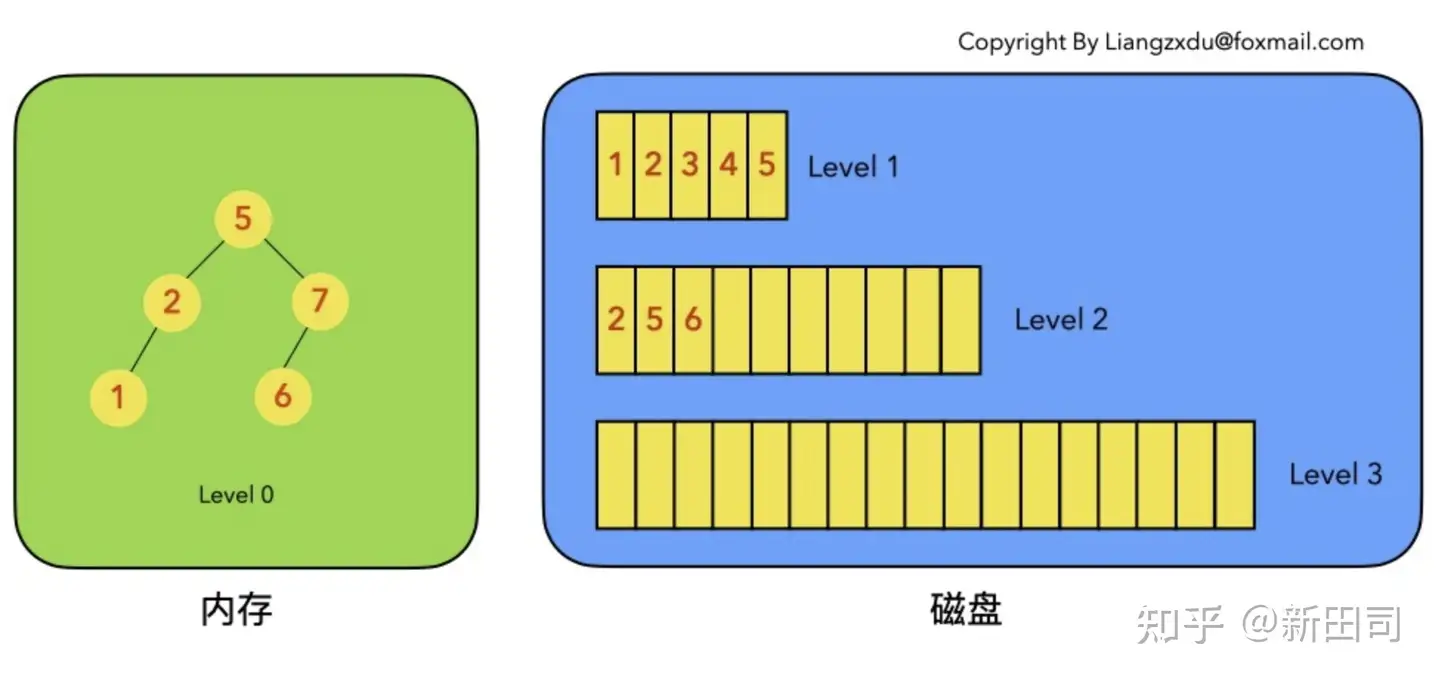
如图所示，左侧部分表示位于内存中的 level-0 结构(一个平衡的排序树)，右侧表示落盘的其他 level。

注意到图中 level-0 到 level-2 中都包含 key 为 2 的数据节点，这是因为上述的性质 5 导致的。

下面开始介绍 LSM-Tree 的增删查改和归并操作：

1. Insert：
   LSM-Tree 的插入一般是直接写到内存中的 level-0 上，并不关心这个数据是否已经存在于磁盘上的 level（如果这个 key 已经存在于 level-0 ，此时的 insert 替换为 update 语义）
   
   插入的时间复杂度一般来说是比较确定的，为 level-0 的树高 logn ，其中 n 为 level-0 的数据量。
2. Delete
   LSM-Tree 的删除一般不是直接删除数据，而是通过给对应节点打上标记来标识数据的删除。
   根据场景不同，一般分为以下三种情况讨论：待删除数据在内存中、待删除数据在磁盘中，待删除数据不存在
   如果待删除数据在内存中，那么用标记标识这个节点。
   如果待删除数据不在内存中，说明要么处于磁盘文件中，要么根本不存在。此时我们也并不需要去磁盘中删除，直接在 level-0 中插入这个节点标识即可。
   
   通过以上分类讨论，发现实际上删除操作都是等价于在 level-0 中写入一个标记，这个复杂度也是比较确定的，为 level-0 的树高 logn，其中 n 为 level-0 的数据量。
3. Update
   按照删除操作的讨论方式，我们将修改操作也分为三类情况讨论
   如果待修改数据在内存中，那么直接在内存的数据结构上覆盖这个节点。
   如果待修改的数据不在内存中，说明要么处于磁盘文件中，要么根本不存在。此时我们并不需要去磁盘中修改，直接在 level-0 中插入这条修改数据即可。
   
   通过以上分类讨论，我们发现修改和删除其实有很多相似的地方，同时复杂度也相对比较容易确定，为 level-0 的树高 logn ，其中 n 为 level-0 的数据量。
4. Get
   LSM-Tree会按照 level-0 到 level-n 的顺序查找每一个 level ，一旦匹配到结果立即返回。这样的好处是保证了查询的结果一定是最新写入的结果，这个性质保障了前面几类写操作结果的正确性(即使多个 level 中存在不同的数据，也可以保证正确性，因为返回的数据可以看作是版本号最高的数据)。
   查找的顺序一般是按照 level-0 采用的数据结构特性做一次遍历，如果不存在的话再去从低到高遍历磁盘上的其他 level 。直到匹配到结果(或者更糟糕的，遍历完所有的 level )。
   可以看出，LSM-Tree虽然能提供非常强大的写吞吐，但是读的性能明显表现较差，虽然可以通过布隆/布谷鸟过滤器+建立索引来优化查询，但是代价明显是大于以 B/B+树为代表的传统存储引擎数据结构的。
5. Compaction(这里以 Tiered Compaction 为例)
   合并操作是 LSM-Tree 这个结构的核心。原因是因为以上一系列机制导致了整个数据结构中存在大量的冗余数据，并且作用于内存的 level-0 也不可能拥有无限的空间。
   一般来说，合并操作可以分为两类情况来讨论：将 level-0 的数据从内存中刷到磁盘中，或是将磁盘中达到阈值的 level 归并到下一 level 中。
   
   对于将内存数据刷到磁盘中的场景：
   将内存中的数据结构有序排列后(例如对于平衡树，取其中序遍历的结果)，顺序的写入 level1 即可，此时 level1 会新增一个 block 。这样能保证新增的 block 是有序的，同时也保证了查询和归并的高效。
   
   对于磁盘中多个 block 的归并：
   由于 block 都是有序的，此时工作类似归并多个有序链表，要注意的是，归并过程中如果遇到相同的 key ，需要保留相对更新的数据，放弃相对更旧的数据。

以上是 LSM-Tree 一般情况下的基本操作。

可以看到，LSM-Tree 的写操作基本都作用于内存上，不仅都拥有相对可靠的时间复杂度保障，且效率都很高，能提供极其优秀的写性能保障。

但是，优异的写表现的 trade-off 是相对更差的读操作，以及为了维护做出的牺牲——Compaction（相较于基于 B/B+树的传统存储引擎而言）

这些 trade-off 带来的问题包括：读放大、写放大、空间放大等，这些问题不仅会导致整个系统的吞吐能力下降，甚至写放大和空间放大这两个问题会明显的作用于硬件成本上，使我们不得不付出更多的机器预算。

对于读操作，我们可以采用布隆/布谷鸟过滤器+建立索引来优化查询。但很遗憾的是，目前针对 LSM-Tree 的研究中，并没有解决 Compaction 问题的完美答案，在单机中，这些代价可以说是不可避免的。不过自1996年 LSM-Tree 诞生以来，无论是工业界还是学术界都提供了很多 Compaction 的优化方向供我们参考。

在下一章《放弃：LSM Tree的Compaction机制探讨和分析》中，将详细分析业界较为流行的 Compaction 策略和一些相关学术研究的成果，并探讨这些成果最终可以带给我们什么。

参考：

深入浅出分析LSM树（日志结构合并树） - 知乎 (zhihu.com)