谢老师2024春 - Day1：组合数学

Day1：组合数学

A - P5520 [yLOI2019] 青原樱

隔板法：

• 已选择的位置：\(m\) 棵樱花树。
• 未选择的位置：\(n-m\) 个空位置
• 板的数量（一棵樱花树就是一个板）：\(m\) 个板子
• 板子可以放在两边，得：\(\tbinom{n-m+1}{m}m!\)

\(\tbinom{n-m+1}{m}m!=\frac{A_{n-m+1}^{m}}{m!}m!=A_{n-m+1}^{m}\)

完事。

#include <bits/stdc++.h>
#define int long long
using namespace std;

int T,n,m,p;
int A(int n,int m,int p){
	int res=1,x=n;
	for(int i=1;i<=m;i++){
		res=(res*x)%p,x--;
	}return res;
}

signed main()
{
    scanf("%lld%lld%lld%lld",&T,&n,&m,&p);
	printf("%lld",A(n-m+1,m,p));
	return 0;
}

---

B - P1313 [NOIP2011 提高组] 计算系数

板子，直接杨辉三角即可，注意需要先把 \(a,b\) 取模一下。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mod=10007;

int C[1005][1005];
int a,b,k,n,m;
int Fast_power(int base,int power){
    int res=1%mod;
    while(power){
        if(power&1) res=(res*base)%mod;
        base=(base*base)%mod;
        power>>=1;
    }
    return res;
}

void Calc_C(int k){
    for(int i=0;i<=k;i++){
        for(int j=0;j<=i;j++){
            if(j==0 or j==i) C[i][j]=1;
            else             C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
        }
    }
}

signed main()
{
    scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m);a%=mod;b%=mod;
    int ans=(Fast_power(a,n)*Fast_power(b,m))%mod;
    Calc_C(k);ans=(ans*C[k][n])%mod;
    printf("%lld",ans);
    return 0;
}

---

C - P3197 [HNOI2008] 越狱

越狱的情况 \(=\) 所有情况 \(-\) 不越狱的情况。

• 所有情况直接幂
• 不越狱的情况，\(A\) 随便选 \(m\) 种，\(B\) 只能选择与 \(A\) 不同的 \(m-1\) 种，\(C\) 只能选与 \(B\) 不同的 \(m-1\) 种 \(\cdots\)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=100003;

int m,n;

int Fast_power(int base,int power){
	int res=1;
	while(power){
		if(power&1) res=(res*base)%mod;
		base=(base*base)%mod;
        power>>=1;
	}return res;
}

signed main()
{
	scanf("%lld%lld",&m,&n);
	int All=Fast_power(m,n);
	int Cant=(m*Fast_power(m-1,n-1))%mod;
    printf("%lld",(mod+All-Cant)%mod);
	return 0;
}

---

D - P2822 [NOIP2016 提高组] 组合数问题

因为每组数据 \(k\) 一定，所以杨辉三角 \(+\) 二维前缀和。

#include <bits/stdc++.h>
using namespace std;

int C[2005][2005],sum[2005][2005];
int T,k,n,m;

void Calc_C(){
    for(int i=0;i<=2000;i++){
        for(int j=0;j<=i;j++){
            if(j==0 or j==i) C[i][j]=1;
            else             C[i][j]=(C[i-1][j-1]+C[i-1][j])%k;
        }
    }
    for(int i=1;i<=2000;i++){
        for(int j=1;j<=i;j++){
            sum[i][j]=(C[i][j]==0)+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
        }sum[i][i+1]=sum[i][i];
    }
}

int main()
{
    scanf("%d%d",&T,&k);Calc_C();
    while(T--){
        scanf("%d%d",&n,&m);
        printf("%d\n",sum[n][min(n,m)]);
    }
    return 0;
}

---

E - P2532 [AHOI2012] 树屋阶梯

考虑递推：\(dp_i\) 表示高度为 \(i\) 的阶梯用 \(i\) 个钢材的搭建方案数。

比如我们以 \(dp_4\) 为例。

注意需要高精度，此处不放高精度模板了，想要完整的板子戳这里

#include <bits/stdc++.h>
using namespace std;

//Some BigInt Code

Bint dp[505];
int N;

int main()
{
    scanf("%d",&N);dp[0]=dp[1]=1;
    for(int i=2;i<=N;i++){
        for(int l1=0,l2=i-1;l1<=i-1;l1++,l2--){
            dp[i]+=dp[l1]*dp[l2];
        }
    }
    cout<<dp[N];
    return 0;
}

---

F - P2290 [HNOI2004] 树的计数

不会。

---

G - P3807 【模板】卢卡斯定理/Lucas 定理

板子。

#include <bits/stdc++.h>
#define int long long
using namespace std;

int Inverse[100005];
int frac[100005];
int T,n,m,p;

int FastPower(int base,int power,int mod){
	int res=1%mod;
	while(power){
		if(power&1) res=1ll*res*base%mod;
		power>>=1;
		base=1ll*(base*base)%mod;
	}return res;
}

void Init(int p){
	memset(frac,0,sizeof(frac));frac[0]=1;
	for(int i=1;i<=p;i++) frac[i]=(1ll*frac[i-1]*i)%p;
	for(int i=1;i<=p;i++) Inverse[i]=FastPower(i,p-2,p);
}

int MiniC(int n,int m){
	if(n<m) return 0;
	else    return (1ll*frac[n]*Inverse[frac[m]]*Inverse[frac[n-m]])%p;
}

int C(int n,int m,int p){
	if(n<p and m<p) return MiniC(n,m)%p;
	else            return (1ll*C(n/p,m/p,p)*MiniC(n%p,m%p))%p;
}

signed main()
{
	scanf("%d",&T);
	while(T--){
		scanf("%d%d%d",&n,&m,&p);Init(p);
		printf("%d\n",C(m+n,n,p));
	}
	return 0;
}

---

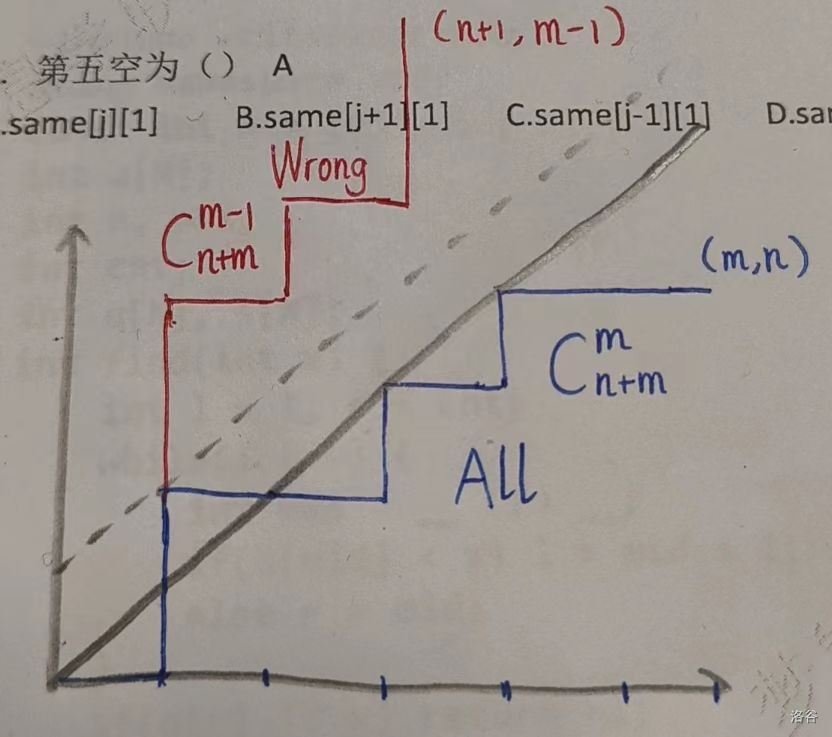
H - P1641 [SCOI2010] 生成字符串

魔改卡特兰数，Lucas 套一套就好了：

#include <bits/stdc++.h>
using namespace std;

int fact[20100405];
int n,m,p;

int FastPower(int base,int power,int mod){
	int res=1;
	while(power){
		if(power&1) res=1ll*res*base%mod;
		base=(1ll*base*base)%mod;
		power>>=1;
	}return res;
}

void Init(){
	memset(fact,0,sizeof(fact));fact[0]=1;
	for(int i=1;i<=n+m;i++) fact[i]=(1ll*fact[i-1]*i)%p;
}

int C(int n,int m){
    int res=1;
    res=(1ll*res*fact[n])%p;
    res=(1ll*res*FastPower(fact[n-m],p-2,p))%p;
    res=(1ll*res*FastPower(fact[m],p-2,p))%p;
    return res;
}

signed main()
{
    scanf("%d%d",&n,&m);p=20100403;Init();
    printf("%d\n",(p+C(n+m,m)-C(m+n,m-1))%p);
	return 0;
}

---

P2480 [SDOI2010] 古代猪文

不会。

---

P3726 [AH2017/HNOI2017] 抛硬币

不会。