Python 实现整数线性规划：分枝定界法（Branch and Bound）

今天做作业，要实现整数线性规划的分枝定界法算法。找了一些网上的博客，发现都很屎，感觉自己写的这个比较清楚、规范，所以在此记录。如有错误，请指正。

from scipy.optimize import linprog
import numpy as np
import math
import sys
from queue import Queue

class ILP():
    def __init__(self, c, A_ub, b_ub, A_eq, b_eq, bounds):
        # 全局参数
        self.LOWER_BOUND = -sys.maxsize
        self.UPPER_BOUND = sys.maxsize
        self.opt_val = None
        self.opt_x = None
        self.Q = Queue()

        # 这些参数在每轮计算中都不会改变
        self.c = -c
        self.A_eq = A_eq
        self.b_eq = b_eq
        self.bounds = bounds

        # 首先计算一下初始问题
        r = linprog(-c, A_ub, b_ub, A_eq, b_eq, bounds)

        # 若最初问题线性不可解
        if not r.success:
            raise ValueError('Not a feasible problem!')

        # 将解和约束参数放入队列
        self.Q.put((r, A_ub, b_ub))

    def solve(self):
        while not self.Q.empty():
            # 取出当前问题
            res, A_ub, b_ub = self.Q.get(block=False)

            # 当前最优值小于总下界，则排除此区域
            if -res.fun < self.LOWER_BOUND:
                continue

            # 若结果 x 中全为整数，则尝试更新全局下界、全局最优值和最优解
            if all(list(map(lambda f: f.is_integer(), res.x))):
                if self.LOWER_BOUND < -res.fun:
                    self.LOWER_BOUND = -res.fun

                if self.opt_val is None or self.opt_val < -res.fun:
                    self.opt_val = -res.fun
                    self.opt_x = res.x

                continue

            # 进行分枝
            else:
                # 寻找 x 中第一个不是整数的，取其下标 idx
                idx = 0
                for i, x in enumerate(res.x):
                    if not x.is_integer():
                        break
                    idx += 1

                # 构建新的约束条件（分割
                new_con1 = np.zeros(A_ub.shape[1])
                new_con1[idx] = -1
                new_con2 = np.zeros(A_ub.shape[1])
                new_con2[idx] = 1
                new_A_ub1 = np.insert(A_ub, A_ub.shape[0], new_con1, axis=0)
                new_A_ub2 = np.insert(A_ub, A_ub.shape[0], new_con2, axis=0)
                new_b_ub1 = np.insert(
                    b_ub, b_ub.shape[0], -math.ceil(res.x[idx]), axis=0)
                new_b_ub2 = np.insert(
                    b_ub, b_ub.shape[0], math.floor(res.x[idx]), axis=0)

                # 将新约束条件加入队列，先加最优值大的那一支
                r1 = linprog(self.c, new_A_ub1, new_b_ub1, self.A_eq,
                             self.b_eq, self.bounds)
                r2 = linprog(self.c, new_A_ub2, new_b_ub2, self.A_eq,
                             self.b_eq, self.bounds)
                if not r1.success and r2.success:
                    self.Q.put((r2, new_A_ub2, new_b_ub2))
                elif not r2.success and r1.success:
                    self.Q.put((r1, new_A_ub1, new_b_ub1))
                elif r1.success and r2.success:
                    if -r1.fun > -r2.fun:
                        self.Q.put((r1, new_A_ub1, new_b_ub1))
                        self.Q.put((r2, new_A_ub2, new_b_ub2))
                    else:
                        self.Q.put((r2, new_A_ub2, new_b_ub2))
                        self.Q.put((r1, new_A_ub1, new_b_ub1))

def test1():
    """ 此测试的真实最优解为 [4, 2] """
    c = np.array([40, 90])
    A = np.array([[9, 7], [7, 20]])
    b = np.array([56, 70])
    Aeq = None
    beq = None
    bounds = [(0, None), (0, None)]

    solver = ILP(c, A, b, Aeq, beq, bounds)
    solver.solve()

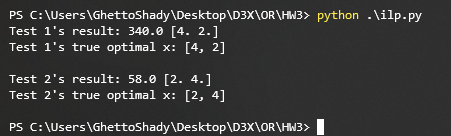
    print("Test 1's result:", solver.opt_val, solver.opt_x)
    print("Test 1's true optimal x: [4, 2]\n")

def test2():
    """ 此测试的真实最优解为 [2, 4] """
    c = np.array([3, 13])
    A = np.array([[2, 9], [11, -8]])
    b = np.array([40, 82])
    Aeq = None
    beq = None
    bounds = [(0, None), (0, None)]

    solver = ILP(c, A, b, Aeq, beq, bounds)
    solver.solve()

    print("Test 2's result:", solver.opt_val, solver.opt_x)
    print("Test 2's true optimal x: [2, 4]\n")

if __name__ == '__main__':
    test1()
    test2()

运行结果截图：