Unity进阶----AssetBundle_03(2018/11/07)

1. 为啥有AB包? 因为资源需要更新, 避免更新一次打包一次 动态修改.

2. AB包注意啥? 依赖关系 找依赖关系应该找到对应的平台!!!

3. 打包策略是分场景打包 若文件被文件夹包含打包出来的就是文件夹的名字 否则是场景文件夹名称

4. 当我AB包从硬盘加载完成之后 是不是就该加载到内存 并实例化了? 带有缓存的ab加载机制

5.脚本不允许出现在打包目录的 dll

6.知道加载的过程 说出来! 这个很重要(依赖加载必须会). 知道框架的基本作用 以后会拿出来用或修改

7. Lua: Lua语言和其他脚本语言有一致特性 Python C很大的渊源 

8.操作步骤:

a. 指定场景

b. 指定abname

c.指定objinabname

d. 协同

e. 委托 void string

f.在委托里面进行物体的实例化操作

 using System.Collections;
 using System.Collections.Generic;
 using UnityEngine;
 using UnityEngine.SceneManagement;
 using LLWHABFW;//引用框架

 public class Scene03Boll : MonoBehaviour {

     private string _abScene = "scenes03";
 //压缩场景的名字---------------------------------->"a"
     private string _abName = "scenes03/scenes03.ab";
 //压缩场景中物体的名字----------------->"b"
     private string _obj01InAB = "Plane.prefab";
 //在scenes03.ab中预制体Plane的名字---------->"c"
     private string _obj02InAB = "Sphere.prefab";
 //在scenes03.ab中预制体Sphere的名字-------->"c"
     private List<GameObject> _mylist;
     void Start()
     {
         _mylist = new List<GameObject>();        StartCoroutine(AssetBundleMgr.GetInstance().LoadAssetBundlePack(_abScene, _abName, heheda));
  //解压所需物体及其依赖-------------------------------------->"d"(参数最后一个为"e")
     }

     void Update ()
     {
         if (Input.GetKeyDown(KeyCode.Space))
         {
             for  (int i=;i<_mylist.Count;i++)
             {
                 Destroy(_mylist[i]);
             }
             _mylist.Clear();

             AssetBundleMgr.GetInstance().DisposeAllAssets(_abScene);
             ABManifestLoader.GetInstance().Dispose();

             StartCoroutine("ssss");
         }
     }
     private void  heheda(string yu)
 //实例化------------------------------------------------>"f"
     {
         GameObject plan, boll;
         plan = AssetBundleMgr.GetInstance().LoadAsset(_abScene, _abName, _obj01InAB, false) as GameObject;
         boll = AssetBundleMgr.GetInstance().LoadAsset(_abScene, _abName, _obj02InAB, false) as GameObject;
        _mylist.Add( Instantiate(plan));
        _mylist.Add(Instantiate(boll));
     }
     IEnumerator ssss()
     {
         yield return new WaitForSeconds();
         SceneManager.LoadScene("");
     }
 }

压缩包对应关系:

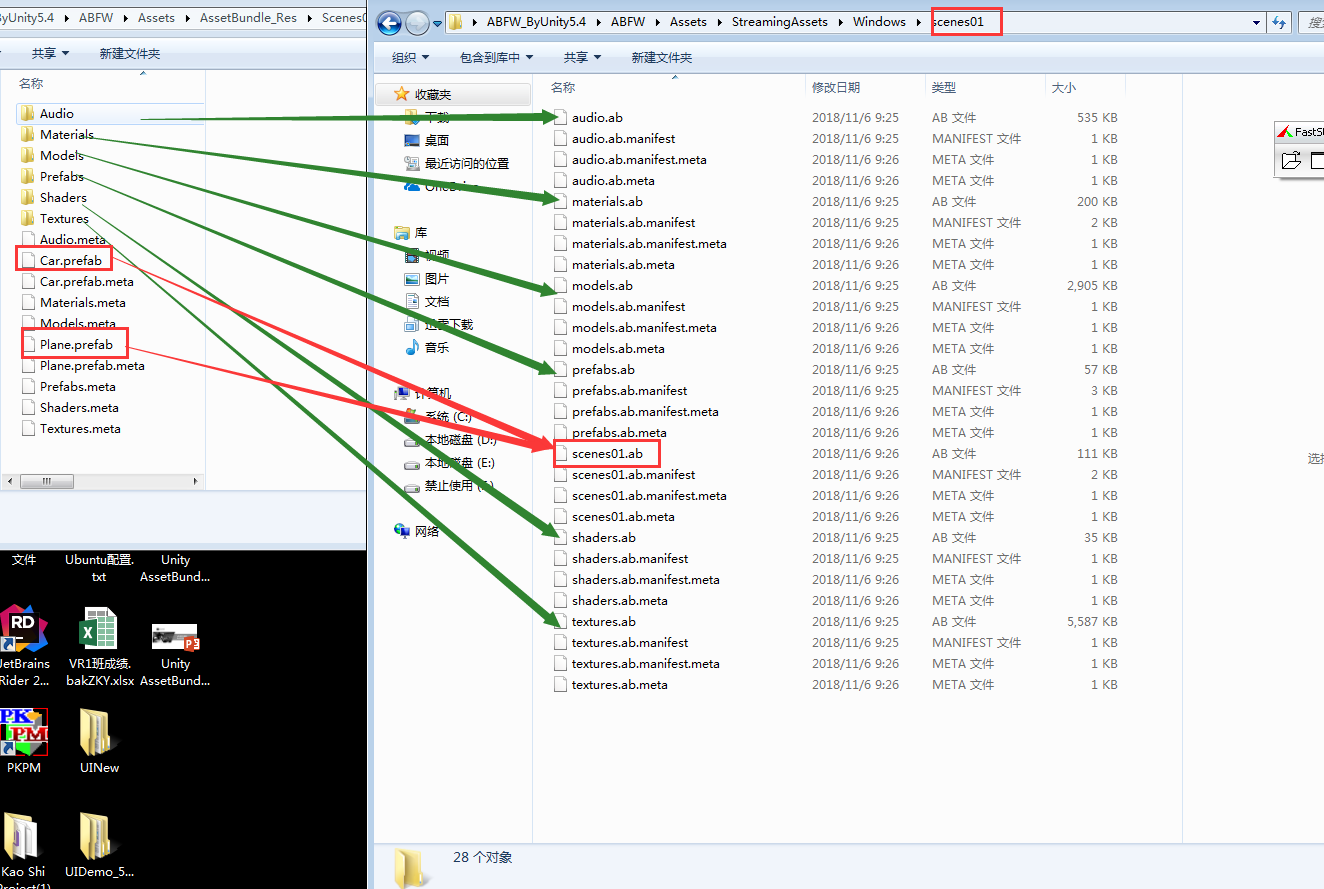
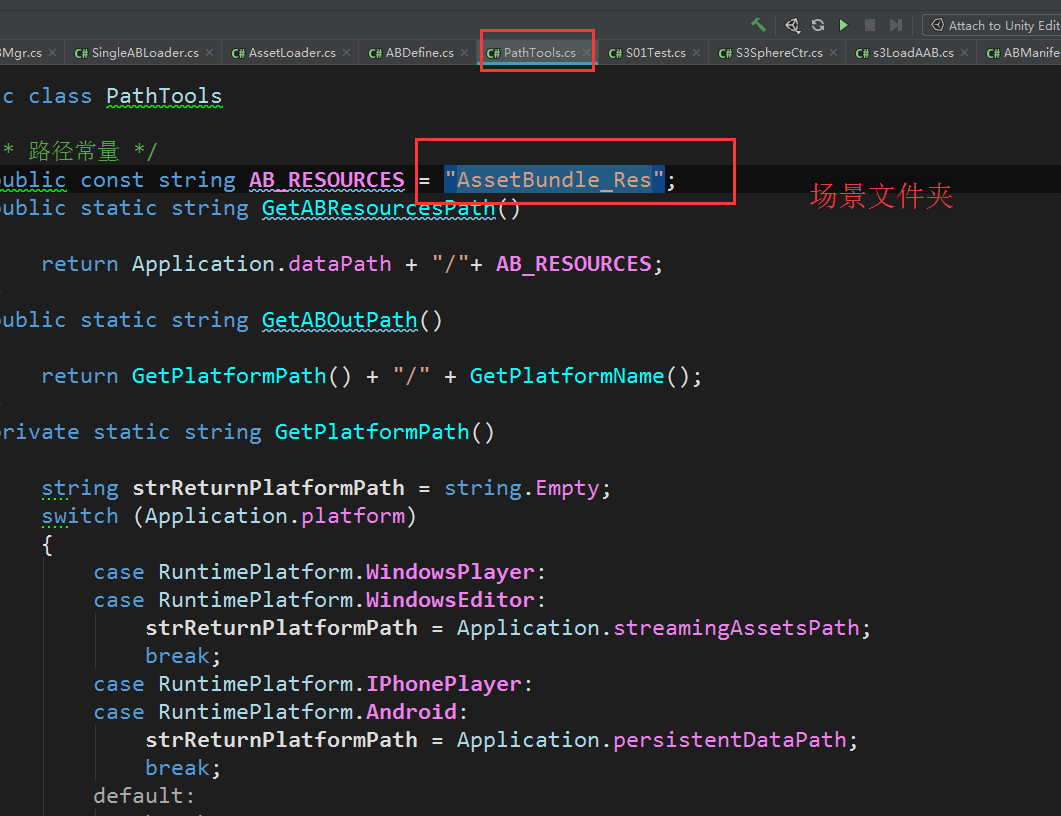
更改路径位置: