P3436 [POI2006]PRO-Professor Szu

P3436 [POI2006]PRO-Professor Szu

题目描述

n个别墅以及一个主建筑楼，从每个别墅都有很多种不同方式走到主建筑楼，其中不同的定义是（每条边可以走多次，如果走边的顺序有一条不同即称两方式不同）。

询问最多的不同方式是多少，以及有多少个别墅有这么多方式，按照顺序输出别墅编号。

如果最多不同方式超过了36500那么都视作zawsze

输入输出样例

输入样例#1：

3 5
1 2
1 3
2 3
3 4
3 4

输出样例#1：

4
1
1

这题反向建个图，缩个点，跑个topo就没了？显然没有这么容易，这里说一下题目的坑点。首先这个题目是要求从n+1号结点出发，那么如果n+1号点不能到达所有的结点会怎么样呢？

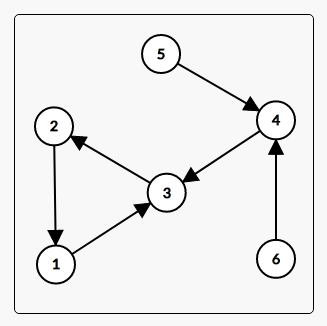
看上面这张图，假设这是我们的反向图，按理说我们应该从6号点开始topo，但是5号点自始至终都不会入队，所以说4号点的入度就不可能减到0，这样的话4号点就无法进行topo,那么这样的答案也肯定是错的。要解决这个问题也很简单，就是在缩点时只缩从n+1号点能到达的结点，然后再建新图，而且建的新图中不能含有从n+1号点不能到达的结点。

 tarjan(n+);//这里只从n+1号点开始缩点
 for(int i=;i<=n+;i++)
 {
     if(!dfn[i]) continue;//如果某一个点是n+1号点无法到达的，那么就不能把这个点加到图中
     for(int j=last[i];j;j=g[j].next)
     {
         int v=g[j].to;
         if(co[i]!=co[v])
         {
             add1(co[i],co[v]);
             de[co[v]]++;
         }
     }
 }

建图

但是这样还是A不了，这又是为啥呢？原来是自环惹的祸。

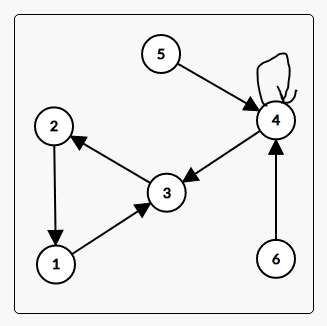
看上边的图，我们已经解决了五号点这个从起点无法到达的点的问题了，但是如果四号点给你来一个自环，那不好意思，你又挂了，要是按正常的缩点的话，四号点应该自己单独成为一个强联通分量，按理应该不需要管他，直接dp就好了，但是如果有自环，那么只要经过4号点，方案数就一定会变为正无穷，所以说，自环也是一定要考虑在内的，但是该怎么做呢，这个就更简单了，只需在读入的时候加个特判就好了，最后统计是把自环也当成环处理即可。

 for(int i=;i<=m;i++)
 {
     aa=read();bb=read();
     if(aa==bb)
     b[aa]=;//如果有自环，就标记一下；
     add(bb,aa);
 }

判断自环

然而这样还是A不了，这究竟是为什么呢？后来经我计算发现36500*1000000=36500000000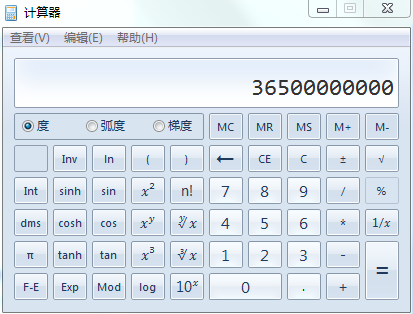

然后就GG了，果断#define int long long，然后就A了……

真的是巨坑无比的一道题目。

 #include<iostream>
 #include<string>
 #include<cmath>
 #include<cstring>
 #include<cstdio>
 #include<stack>
 #include<queue>
 #define int long long
 #define maxn 2000005
 using namespace std;

 struct edge
 {
     int next,to;
 }g[maxn<<],g1[maxn<<];
 int n,m,num,tot,col,num1,aa,bb,cnt,tott,pd,de[maxn],t[maxn];
 long long ans;
 long long f[maxn];
 int last[maxn],dfn[maxn],low[maxn],co[maxn],last1[maxn],a[maxn],b[maxn],c[maxn];
 stack<int>s;
 stack<int>ss;

 inline int read()
 {
     char c=getchar();
     int x=,res=;
     while(c<''||c>'')
     {
         if(c=='-')
         x=-;
         c=getchar();
     }
     while(c>=''&&c<='')
     {
         res=res*+(c-'');
         c=getchar();
     }
     return x*res;
 }

 void add(int from,int to)
 {
     g[++num].next=last[from];
     g[num].to=to;
     last[from]=num;
 }

 void add1(int from,int to)
 {
     g1[++num1].next=last1[from];
     g1[num1].to=to;
     last1[from]=num1;
 }

 void tarjan(int u)
 {
     dfn[u]=low[u]=++tot;
     s.push(u);
     for(int i=last[u];i;i=g[i].next)
     {
         int v=g[i].to;
         if(!dfn[v])
         {
             tarjan(v);
             low[u]=min(low[u],low[v]);
         }
         else if(!co[v])
         {
             low[u]=min(low[u],dfn[v]);
         }
     }
     if(low[u]==dfn[u])
     {
         col++;cnt=;
         for(;;)
         {
             int x=s.top();s.pop();
             co[x]=col;
             cnt++;
             if(x==u) break;
         }
         a[col]=cnt;
     }
 }

 void topo()
 {
     ss.push(co[n+]);
     if(c[co[n+]]==)
     {
         f[co[n+]]=;
     }
     else
     {
         f[co[n+]]=;
     }
     while(ss.size())
     {
         int u=ss.top();ss.pop();
         for(int i=last1[u];i;i=g1[i].next)
         {
             int v=g1[i].to;
             if(c[v]==)
             {
                 f[v]=;
             }
             else
             {
                 f[v]+=f[u];
             }
             de[v]--;
             if(de[v]==)
             ss.push(v);
         }
     }
 }

 signed main()
 {
     n=read();m=read();
     for(int i=;i<=m;i++)
     {
         aa=read();bb=read();
         if(aa==bb)
         b[aa]=;//如果有自环，就标记一下；
         add(bb,aa);
     }
     tarjan(n+);//这里只从n+1号点开始缩点
     for(int i=;i<=n+;i++)
     {
         if(!dfn[i]) continue;//如果某一个点是n+1号点无法到达的，那么就不能把这个点加到图中
         for(int j=last[i];j;j=g[j].next)
         {
             int v=g[j].to;
             if(co[i]!=co[v])
             {
                 add1(co[i],co[v]);
                 de[co[v]]++;
             }
         }
     }
     for(int i=;i<=n+;i++)
     {
         if(b[i]==)
         {
             c[co[i]]=;
         }
         if(a[co[i]]>)
         {
             c[co[i]]=;
         }
     }
     topo();
     for(int i=;i<=n;i++)
     {
         if(f[co[i]]>)
         {
             pd=;
         }
         ans=max(ans,f[co[i]]);
     }
     if(pd==)
     {
         printf("zawsze\n");
         for(int i=;i<=n;i++)
         {
             if(f[co[i]]>)
             {
                 t[++tott]=i;
             }
         }
         printf("%d\n",tott);
         for(int i=;i<=tott;i++)
         {
             printf("%d ",t[i]);
         }
         return ;
     }
     else
     {
         printf("%lld\n",ans);
         for(int i=;i<=n;i++)
         {
             if(f[co[i]]==ans)
             t[++tott]=i;
         }
         printf("%d\n",tott);
         for(int i=;i<=tott;i++)
         {
             printf("%d ",t[i]);
         }
         return ;
     }
 }