Verilog笔记.3.有限状态机

有限状态机
有限状态机是由寄存器组和组合逻辑构成的硬件时序电路，其状态（即由寄存器组的1和0的组合状态
所构成的有限个状态）只可能在同一时钟跳变沿的情况下才能从一个状态转向另一个状态，究竟转向
哪一状态还是留在原状态不但取决于各个输入值，还取决于当前所在状态。（这里指的是米里Mealy型有限状态
机，而莫尔Moore型有限状态机究竟转向哪一状态只决于当前状态。）

例

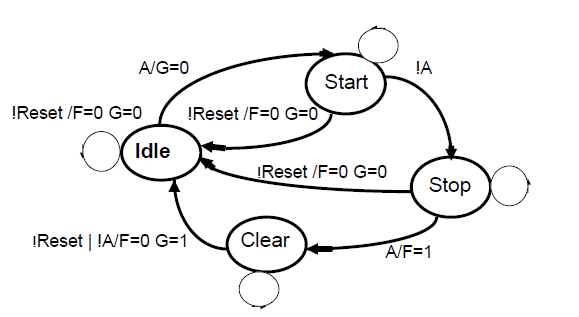
采用独热码实现的有限状态机。采用了独热编码后有了多余的状态，就有一些不可到达的状态，为此在CASE语句的最后需要增加default分支项，以确保多余状态能回到Idle状态。

 module fsm (Clock, Reset, A, F, G);
 input Clock, Reset, A;
 output F,G;
 reg F,G;
 reg [:] state ;
 parameter Idle = ’b1000,
 Start = ’b0100,
 Stop = ’b0010,
 Clear = ’b0001;
 always @(posedge clock)
     if (!Reset)
     begin
         state <= Idle; F<=; G<=;
     end
     else
     case (state)
         Idle: begin
             if (A) begin
                 state <= Start;
                 G<=;
             end
             else state <= Idle;
         end
         Start: if (!A) state <= Stop;
             else state <= Start;
         Stop: begin
             if (A) begin
                 state <= Clear;
                 F <= ;
             end
             else state <= Stop;
         end
         Clear: begin
             if (!A) begin
             state <=Idle;
             F<=; G<=;
             end
             else state <= Clear;
         end
         default: state <=Idle;
     endcase
 endmodule                                        

用always语句和连续赋值语句把状态机的触发器部分和组合逻辑部分分成两部分来描述。

 module fsm (Clock, Reset, A, F, G);
 input Clock, Reset, A;
 output F,G;

 reg [:] state ;
 wire [:] Nextstate;
 parameter     Idle = ’b00,
             Start = ’b01,
             Stop = ’b10,
             Clear = ’b11;

 always @(posedge Clock)
 begin
     if (!Reset)
     begin
     state <= Idle;
     end
     else
     state <= Nextstate;
 end

 assign Nextstate =     ( state == Idle ) ? ( A ? Start : Idle ) :
                     ( state==Start ) ? ( !A ? Stop : Start ) :
                     ( state== Stop ) ? ( A ? Clear : Stop ) :
                     ( state== Clear) ? ( !A ? Idle : Clear) :
                     Idle;
 assign F = (( state == Stop) && A );
 assign G = (( state == Clear) && (!A || !Reset));

 endmodule

用沿触发的always语句和电平敏感的always语句把状态机的触发器部分和组合逻辑部分分成两部分来描述。

 module fsm (Clock, Reset, A, F, G);
 input Clock, Reset, A;
 output F,G;

 reg [:] state, Nextstate;
 parameter     Idle = ’b00,
             Start = ’b01,
             Stop = ’b10,
             Clear = ’b11;

 always @(posedge Clock)
 begin
     if (!Reset)
     begin
         state <= Idle;
     end
     else
         state <= Nextstate;
 end

 always @( state or A )
 begin
     F=;
     G=;
     if (state == Idle)
     begin
         if (A)
             Nextstate = Start;
         else
             Nextstate = Idle;
         G=;
     end
     else
         if (state == Start)
             if (!A)
                 Nextstate = Stop;
             else
                 Nextstate = Start;
         else
             if (state == Stop)
                 if (A)
                     Nextstate = Clear;
                 else
                     Nextstate = Stop;
             else
                 if (state == Clear)
                 begin
                     if (!A)
                         Nextstate = Idle;
                     else
                         Nextstate = Clear;
                     F=;
                 end
                 else
                     Nextstate= Idle;
     end
 end
 endmodule

状态必须明确赋值，通常使用参数(parameters)或宏定义(define)语句加上赋值语句来实现。

原则 1：时序电路建模时，用非阻塞赋值。
原则 2：锁存器电路建模时，用非阻塞赋值。
原则 3：用always 块写组合逻辑时，采用阻塞赋值。
原则 4：在同一个always 块中同时建立时序和组合逻辑电路时，用非阻塞赋值。
原则 5：在同一个always 块中不要同时使用非阻塞赋值和阻塞赋值。
原则 6：不要在多个always 块中为同一个变量赋值。