ownCloud 的六大神奇用法

ownCloud 是一个自行托管的开源文件同步和共享服务器。就像“行业老大” Dropbox、Google Drive、Box 和其他的同类服务一样，ownCloud 也可以让你访问自己的文件、日历、联系人和其他数据。

你可以在自己设备之间同步任意数据（或部分数据）并分享给其他人。然而，ownCloud 要比其它的商业解决方案更棒，可以将 ownCloud 运行在自己的服务器而不是其它人的服务器上。

现在，让我们一起来看看在 ownCloud 上的六个创造性的应用方式。其中一些是由于 ownCloud 的开源才得以完成，而另外的则是 ownCloud 自身特有的功能。

1. 可扩展的 ownCloud “派”集群

由于 ownCloud 是开源的，你可以选择将它运行在自己的服务器中，或者从你信任的服务商那里获取空间——没必要将你的文件存储在那些大公司的服务器中，谁知他们将你的文件存储到哪里去。

拍摄： Jörn Friedrich Dreyer. CC BY-SA 4.0.

我们见过最具创意的事情就是架设香蕉派集群和树莓派集群。ownCloud 的扩展性通常用于支持成千上万的用户，但有些人则将它往不同方向发展，通过将多个微型系统集群在一起，就可以创建出运行速度超快的 ownCloud。酷毙了！

2. 密码同步

为了让 ownCloud 更容易扩展，我们将它变得超级的模块化，甚至还有一个 ownCloud 应用商店。你可以在里边找到音乐和视频播放器、日历、联系人、生产力应用、游戏、应用模板等等。

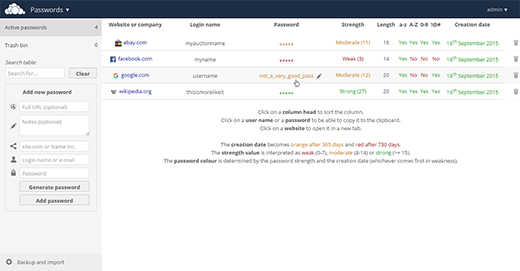
从近 200 多个应用中仅挑选一个是一件非常困难的事，但密码管理则是一个很独特的功能。只有不超过三个应用提供这个功能：Passwords、Secure Container 和 Passman。

3. 随心所欲地存储文件

外部存储可以让你将现有数据挂载到 ownCloud 上，让你通过一个界面来访问存储在 FTP、WebDAV、Amazon S3，甚至 Dropbox 和 Google Drive 的文件。

行业老大们喜欢创建自己的 “藩篱花园”，Box 的用户只能和其它的 Box 用户协作；假如你想从 Google Drive 分享你的文件，你的同伴也必须要有一个 Google 账号才可以访问的分享。通过 ownCloud 的外部存储功能，你可以轻松打破这些。

最有创意的就是把 Google Drive 和 Dropbox 添加为外部存储。这样你就可以无缝连接它们，通过一个简单的链接即可分享给其它人——并不需要账户。

4. 获取上传的文件

由于 ownCloud 是开源开，人们可以不受公司需求的制约而向它贡献感兴趣的功能。我们的贡献者总是很在意安全和隐私，所以 ownCloud 引入的通过密码保护公共链接并设置失效期限的功能要比其它人早很多。

现在，ownCloud 可以配置分享链接的读写权限了，这就是说链接的访问者可以无缝的编辑你分享给他们的文件（可以有密码保护，也可以没有），或者将文件上传到服务器前不用强制他们提供私人信息来注册服务。

对于有人想给你分享大体积的文件时，这个特性就非常有用了。相比于上传到第三方站点、然后给你发送一个连接、你再去下载文件（通常需要登录），ownCloud 仅需要上传文件到你提供的分享文件夹，你就可以马上获取到文件了。

5. 免费却又安全的存储空间

之前就强调过，我们的代码贡献者最关注的就是安全和隐私，这就是 ownCloud 中有用于加密和解密存储数据的应用的原因。

通过使用 ownCloud 将你的文件存储到 Dropbox 或者 Google Drive，则会违背夺回数据的控制权并保持数据隐私的初衷。但是加密应用则可以改变这个状况。在发送数据给这些提供商前进行数据加密，并在取回数据的时候进行解密，你的数据就会变得很安全。

6. 在你的可控范围内分享文件

作为开源项目，ownCloud 没有必要自建 “藩篱花园”。通过“联邦云共享”：这个由 ownCloud 开发和发布的协议使不同的文件同步和共享服务器可以彼此之间进行通信，并能够安全地传输文件。联邦云共享本身来自一个有趣的事情：有 22 所德国大学 想要为自身的 50 万名学生建立一个庞大的云服务，但是每个大学都想控制自己学生的数据。于

是乎，我们需要一个创造性的解决方案：也就是联邦云服务。该解决方案可以连接全部的大学，使得学生们可以无缝的协同工作。同时，每个大学的系统管理员保持着对自己学生创建的文件的控制权，并可采用自己的策略，如限制限额，或者限制什么人、什么文件以及如何共享。

并且，这项神奇的技术并没有限制于德国的大学之间，每个 ownCloud 用户都能在自己的用户设置中找到自己的联邦云 ID，并将之分享给同伴。

现在你明白了吧。通过这六个方式，ownCloud 就能让人们做一些特殊而独特的事。而使这一切成为可能的，就是 ownCloud 是开源的，其设计目标就是让你的数据自由。

本文转载地址：https://www.linuxprobe.com/owncloud-six-artifact.html