Codeforces 931.F Teodor is not a liar!

F. Teodor is not a liar!

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Young Teodor enjoys drawing. His favourite hobby is drawing segments with integer borders inside his huge [1;m] segment. One day Teodor noticed that picture he just drawn has one interesting feature: there doesn't exist an integer point, that belongs each of segments in the picture. Having discovered this fact, Teodor decided to share it with Sasha.

Sasha knows that Teodor likes to show off so he never trusts him. Teodor wants to prove that he can be trusted sometimes, so he decided to convince Sasha that there is no such integer point in his picture, which belongs to each segment. However Teodor is lazy person and neither wills to tell Sasha all coordinates of segments' ends nor wills to tell him their amount, so he suggested Sasha to ask him series of questions 'Given the integer point xi, how many segments in Fedya's picture contain that point?', promising to tell correct answers for this questions.

Both boys are very busy studying and don't have much time, so they ask you to find out how many questions can Sasha ask Teodor, that having only answers on his questions, Sasha can't be sure that Teodor isn't lying to him. Note that Sasha doesn't know amount of segments in Teodor's picture. Sure, Sasha is smart person and never asks about same point twice.

Input

First line of input contains two integer numbers: n and m (1 ≤ n, m ≤ 100 000) — amount of segments of Teodor's picture and maximal coordinate of point that Sasha can ask about.

ith of next n lines contains two integer numbers li and ri (1 ≤ li ≤ ri ≤ m) — left and right ends of ith segment in the picture. Note that that left and right ends of segment can be the same point.

It is guaranteed that there is no integer point, that belongs to all segments.

Output

Single line of output should contain one integer number k – size of largest set (xi, cnt(xi)) where all xi are different, 1 ≤ xi ≤ m, and cnt(xi) is amount of segments, containing point with coordinate xi, such that one can't be sure that there doesn't exist point, belonging to all of segments in initial picture, if he knows only this set(and doesn't know n).

Examples

input

Copy

2 4
1 2
3 4

output

4

input

Copy

4 6
1 3
2 3
4 6
5 6

output

5

Note

First example shows situation where Sasha can never be sure that Teodor isn't lying to him, because even if one knows cnt(xi) for each point in segment [1;4], he can't distinguish this case from situation Teodor has drawn whole [1;4] segment.

In second example Sasha can ask about 5 points e.g. 1, 2, 3, 5, 6, still not being sure if Teodor haven't lied to him. But once he knows information about all points in [1;6] segment, Sasha can be sure that Teodor haven't lied to him.

题目大意：有一条线段，上面的点被若干条线段覆盖着. Sasha想知道是否存在一个整点被所有的线段覆盖，她每次可以任选一个点，Teodor会告诉她这个点被多少个线段覆盖，但是Sasha不知道有多少条线段.求Sasha最多猜多少次还不知道这个问题的答案. 也就是说，如果你最多猜n次能知道答案，那么输出n-1.如果猜不到答案就输出n.

分析：这种题目把图一画，各种情况考虑一下就能做出来了.

　　　什么情况下Sasha能知道答案呢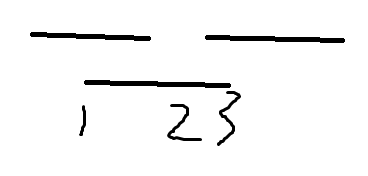？ 在这幅图中,1,2,3都被猜过了，覆盖2的线段数小于覆盖1,3的，而线段是连续的，说明有线段到2这个点就中断了，自然就没有整点被所有的线段给覆盖了. 同样的，如果覆盖2的线段数大于覆盖1,3的，也是能够猜出来的. 为了使猜的次数最多，把1,3全都猜完就行了.

　　　所以究竟是求什么呢? 要求猜的数组成的子序列中不能有两个凸起的部分，只能一边是单调函数，另一边也是单调函数.那么就是要求一个最长的单峰子序列.树状数组扫两次就好了.

　　　小细节：树状数组查询，修改的数不能是0，而这道题中可能存在点没有被线段覆盖，所以要默认有一条线段覆盖了所有点.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = ;
int n,m,c1[maxn],c2[maxn],a[maxn],sum,f1[maxn],f2[maxn],ans;

int add1(int x,int v)
{
    while (x <= n)
    {
        c1[x] = max(c1[x],v);
        x += x & (-x);
    }
}

int query1(int x)
{
    int res = ;
    while (x)
    {
        res = max(res,c1[x]);
        x -= x & (-x);
    }
    return res;
}

int add2(int x,int v)
{
    while (x <= n)
    {
        c2[x] = max(c2[x],v);
        x += x & (-x);
    }
}

int query2(int x)
{
    int res = ;
    while (x)
    {
        res = max(res,c2[x]);
        x -= x & (-x);
    }
    return res;
}

int main()
{
    scanf("%d%d",&n,&m);
    for (int i = ; i <= n; i++)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        a[l]++;
        a[r + ]--;
    }
    for (int i = ; i <= m; i++)
    {
        sum += a[i];
        a[i] = sum + ;
    }
    for (int i = ; i <= m; i++)
    {
        f1[i] = query1(a[i]) + ;
        add1(a[i],f1[i]);
    }
    for (int i = m; i >= ; i--)
    {
        f2[i] = query2(a[i]) + ;
        add2(a[i],f2[i]);
    }
    for (int i = ; i <= m; i++)
        ans = max(ans,f1[i] + f2[i] - );
    printf("%d\n",ans);

    return ;
}