cryptohack wp day(3)

第二节模运算----第一题（ GCD ）

在做这道题前，了解下欧几里得算法：

欧几里得算法，也叫辗转相除法，用于求解两个非负整数a和b的最大公约数（Greatest Common Divisor, GCD），即能够同时整除它们的最大正整数。

算法的基本思想是，通过不断求解a和b的余数的最大公约数，最终可以得到a和b的最大公约数。

具体地，设r为a除以b的余数，则有：

a = bq + r

其中，q为a除以b的商。如果r等于0，则b就是a和b的最大公约数；否则，继续使用同样的方法求解b和r的最大公约数。直到r等于0为止，此时的b就是a和b的最大公约数

以下是Python实现该算法的代码：

a = 66528
b = 52920

def gcd(a, b):  #欧几里得算法
    if b == 0:
        return a
    else:
        return gcd(b, a % b)

print(gcd(a,b))

第二题（Extended GCD）

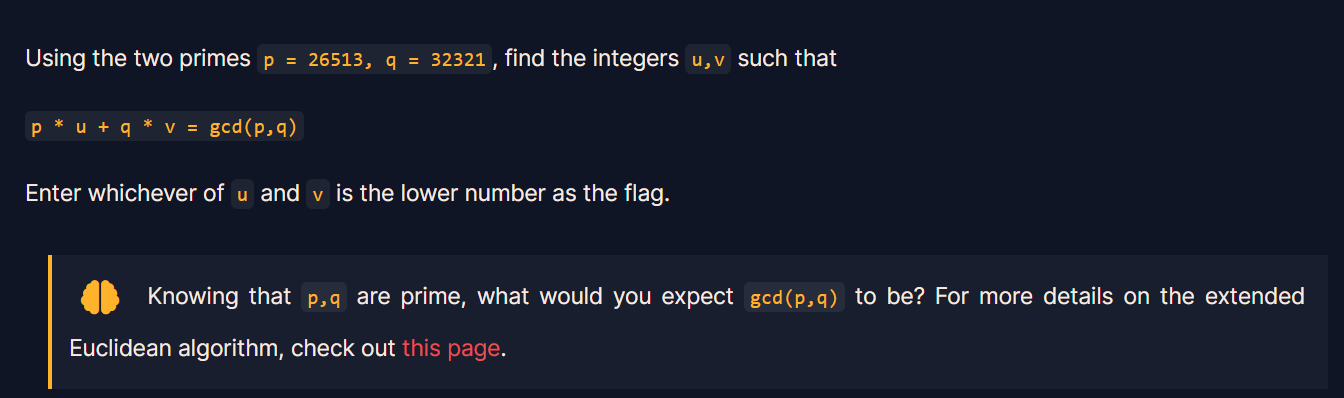
在进行这道题之前，先了解下扩展欧几里得算法吧：

扩展欧几里得算法是求解两个整数a、b的最大公约数（Greatest Common Divisor, GCD）以及一组整数x、y，使得它们满足以下等式：

ax + by = gcd(a,b)

其中，x、y是整数，gcd(a,b)表示a、b的最大公约数。

该算法的基本思想是利用欧几里得算法递归求解gcd(a,b)，并在递归的过程中同时求解x、y的值。

具体地，假设我们已经求得了b和a%b（即a除以b的余数）的最大公约数gcd(b, a%b)，并得到了一组整数x1、y1，使得：

bx1 + (a%b)y1 = gcd(b, a%b)

接下来，我们可以将a%b表示为a-b(a//b)，其中a//b表示a除以b的商，将其带入上式得：

bx1 + (a - b(a//b))y1 = gcd(b, a%b)

移项可得：

ay1 + b(x1 - (a//b)y1) = gcd(b, a%b)

由此可以得到a和b的最大公约数gcd(a,b)和一组整数x、y，使得：

ax + by = gcd(a,b)

其中：

gcd(a,b) = gcd(b, a%b)

x = y1

y = x1 - (a//b)*y1

最终的结果是递归求解出gcd(a,b)的同时求得了x和y的值。

以下是python代码实现：

def egcd(a, b):  #扩展欧几里得算法
    if b == 0:
        return (a, 1, 0)
    else:
        gcd, x1, y1 = egcd(b, a % b)
        x = y1
        y = x1 - (a // b) * y1
        return (gcd, x, y)
print(egcd(a,b))

第三题（Modular Arithmetic 1）

分析下吧，先说下同余

同余“≡”是数论中表示同余的符号

同余的定义如下

给定一个正整数m，如果两个整数a和b满足a-b能被m整除，即(a-b)modm=0，那么就称整数a与b对模m同余，记作a≡b(modm)，同时可成立amodm=b

再次提醒注意，同余与模运算是不同的，a≡b(modm)仅可推出b=amodm

对于第一个问题，我们需要找到一个整数x，使得11和x在模6下是同余的。因为6是一个较小的数，我们可以手动计算11除以6的余数，然后将余数减去11，直到得到一个小于6的余数。这样的余数就是我们要找的x。

11除以6的商是1，余数是5，因此我们可以将11减去5，得到6，这是6的一个倍数，因此我们可以得出11 ≡ 5 模 6。由于5是小于6的，因此5是我们要找的最小非负整数x。

对于第二个问题，我们需要找到一个整数y，使得8146798528947和y在模17下是同余的。因为这个数太大，我们需要使用计算器来进行计算。

我们可以使用Python中的模运算符号%来计算这个问题。具体来说，我们可以计算8146798528947除以17的余数，这样的余数就是我们要找的y。Python代码如下：

y = 8146798528947 % 17

计算结果是4，因此8146798528947 ≡ 4 模 17。因为4是小于17的，因此4是我们要找的最小非负整数y。

因此，x = 5，y = 4是这两个问题的答案。

第四题（Modular Arithmetic 2）

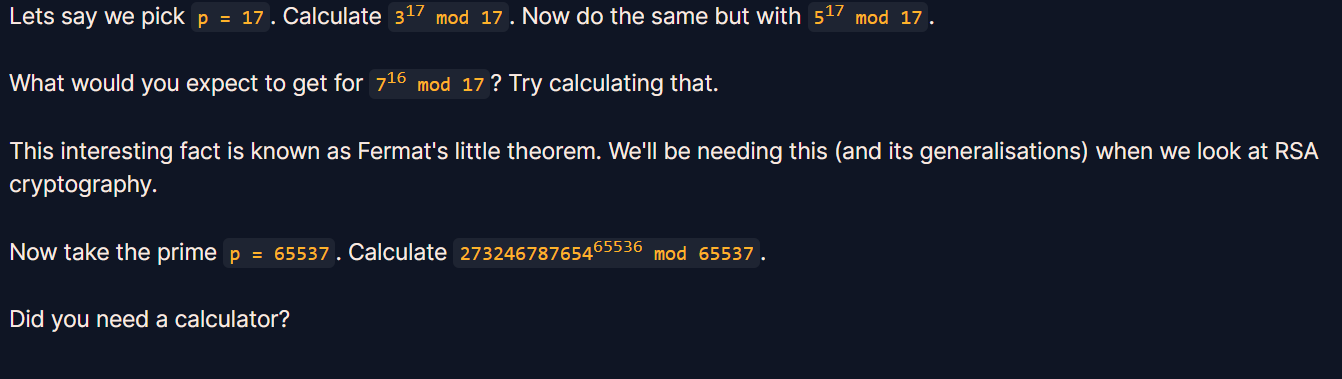
在学习这道题之前，先了解下费马定理吧，如下：

费马定理是数论中的一个基本定理，由法国数学家皮埃尔·德·费马于17世纪提出。该定理的原始形式是：对于任何素数p和任何不是p的倍数的正整数a，a的p-1次方减去1能够被p整除，即a^(p-1) ≡ 1 (mod p)。

换句话说，如果p是一个素数，那么对于任何不是p的倍数的正整数a，a的p-1次方对p取模的结果为1。这个定理的一个重要应用是在密码学中的RSA算法，其中大素数的选取基于费马定理。

费马定理的证明较为复杂，这里不再赘述。值得一提的是，当p是一个合数（即非素数）时，费马定理并不成立，这是因为如果p是一个合数，那么a^(p-1)除以p的余数可能不为1，例如，当a=2，p=15时，2^14 ≡ 1 (mod 15)不成立。

回到这道题，273246787654^65536 mod 65537,根据费马定理a^(p-1) ≡ 1 (mod p)，取p=65537，则在进行模运算273246787654 % 65537 =1，即答案为1.