NOI P序列题 （二分）

题面

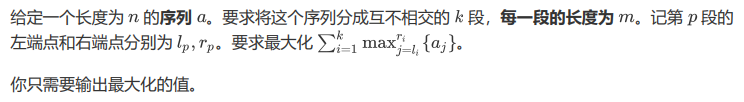
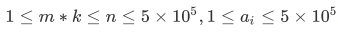
题解

——WQS二分

想到这个这题就完了。

赛时没想到这个你就完了。

时间复杂度

O

(

n

log

⁡

a

)

O(n\log a)

O(nloga)

---

不难发现这题有凸性，可以WQS二分。

我们把只能选 k 个段的限制去掉，二分一个罚款额，每次多选一个段，贡献就要罚款，这样可以调整到选 k 个的答案。

最后把罚款后的贡献再加上 k × 罚款额。

---

去掉限制也不会？

d

p

[

i

]

dp[i]

dp[i] 表示前

i

i

i 个最优答案即可。同时别忘了记录段数（的最值）。

---

没在NOI考纲上啊，所以还是有可能考的

CODE

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<bitset>
#include<random>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 500005
#define LL long long
#define DB double
#define ENDL putchar('\n')
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second

namespace{

	LL read() {
		LL f=1,x=0;int s = getchar();if(s < 0) return -1;
		while(s < '0' || s > '9') {if(s == '-')f=-f;s = getchar();}
		while(s >= '0' && s <= '9') {x=x*10+(s^48);s = getchar();}
		return f * x;
	}
	void putpos(LL x) {if(!x)return ;putpos(x/10);putchar('0'+(x%10));}
	void putnum(LL x) {
		if(!x) {putchar('0');return ;}
		if(x<0) {putchar('-');x = -x;}
		return putpos(x);
	}
	void AIput(LL x,int c) {putnum(x);putchar(c);}

	int n,m,s,o,k;
	int a[MAXN],b[MAXN];
	int f[MAXN],st[MAXN],hd,tl;
	LL dp[MAXN],ct[MAXN],ans;
	int heck(LL ad) {
		for(int i = 1;i <= n;i ++) {
			dp[i] = 0;ct[i] = 0;
		}
		dp[0] = 0; ct[0] = 0;
		for(int i = m;i <= n;i ++) {
			dp[i] = dp[i-1]; ct[i] = ct[i-1];
			if(dp[i-m] + f[i]+ad > dp[i] || (dp[i-m]+f[i]+ad == dp[i] && ct[i-m]+1 > ct[i])) {
				dp[i] = dp[i-m]+f[i]+ad; ct[i] = ct[i-m]+1;
			}
		}
		ans = dp[n];
		return ct[n];
	}

}
int main() {
	n = read();m = read();k = read();
	st[hd = 1] = 0; tl = 0;
	for(int i = 1;i <= n;i ++) {
		a[i] = read();
		while(hd <= tl && a[st[tl]] < a[i]) st[tl --] = 0;
		st[++ tl] = i;
		if(st[hd] <= i-m) st[hd ++] = 0;
		f[i] = a[st[hd]];
	}
	int l = -500000,r = 500000,md;
	while(l < r) {
		md = floor((l+r)/2.0);
		if(heck(md) >= k) r = md;
		else l = md+1;
	}
	int cn = heck(l);
	ans -= l*1ll*k;
	AIput(ans,'\n');
	return 0;
}