(Bezier)贝塞尔曲在路径规划的运用

前言

之前被安排了活，一个局部区域机器运动控制的工作，大致是一个机器位于一个极限区域时候，机器要进入一个特殊的机制，使得机器可以安全的走出来。其中用到了bezier曲线进行优化路径，今天写一下，正好也给大家分享一下工作和实践的情况。

作者：良知犹存

转载授权以及围观：欢迎关注微信公众号：羽林君

或者添加作者个人微信：become_me

---

贝塞尔曲线基本介绍

线段都可以被拆分成两个坐标的差来表示,如下面一阶的贝塞尔曲线，P0到P1，可以用一个t进行拆分这段线,分别是线段 t(P0～P1)、线段 1-t(P0～P1)，P0和P1叫做， 这条条贝塞尔的两个控制点，而贝塞尔曲线至少要有两个控制点（就是下面的这条直线，一阶贝塞尔曲线）。在贝塞尔曲线与控制点位置相关，这意味着在曲线生成过程中，我们可以通过调节控制点的位置，进而调整整个曲线。

贝塞尔的阶数和次数是一样的，二阶贝塞尔，三个点，最高次数二次。例：二阶贝塞尔：三个点，两个线段，以所有等比的点组合成的曲线叫做二阶贝塞尔曲线。

接下来给大家介绍一下贝塞尔曲线的推导工程，也比较简单，并且网上的介绍也挺多的：

一阶：

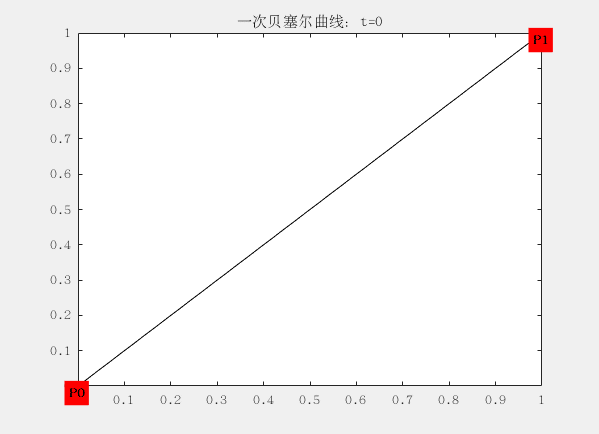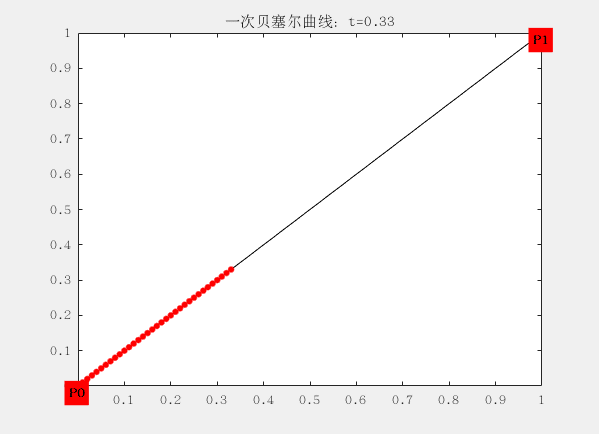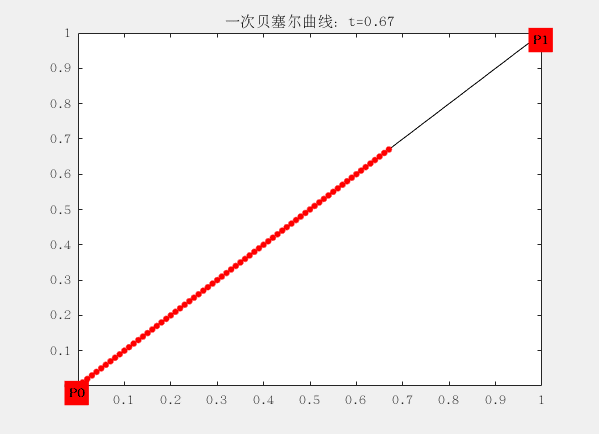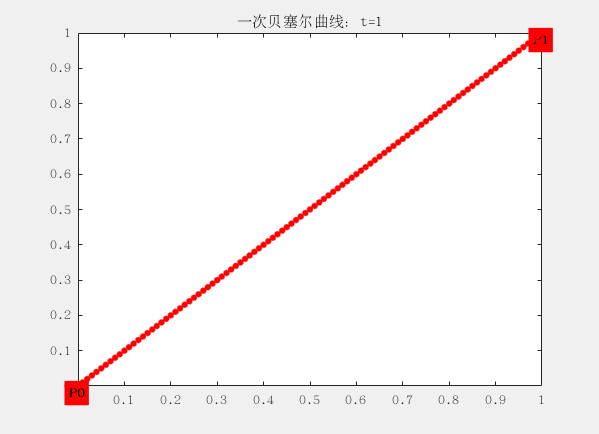
这里面有两个控制点为$ P_0 (0,0) 和P_1 (1,1)$ ，对应的曲线方程为：

$$ B\big( t \big) = P_t = (1 - t) P_0 + tP_1 = P_0 + (P_1 - P_0)t $$

tϵ[0,1]

这个方程可以理解为，从$P_0$出发，朝着$P_1$的方向前进$||P_1-P_0||t$的距离，从而得到了点B(t)的位置。t从0逐渐递增到1，这个过程完成，就成了我们所看到的曲线。

另外，之所以是一阶贝塞尔曲线是因为方程是关于t的一阶多项式，多阶也是一样。

二阶：

有三个控制点，这里的 P0、P1、P2 分别称之为控制点，曲线的产生完全与这三个点位置相关。

与一阶有些区别就在于三个控制点形成两个线段，每个线段上有一个点在运动，于是得到两个点；

再使用两个点形成一个线段，这个线段上有一个点在运动，于是得到一个点；最后一个点的运动轨迹便构成了二阶贝塞尔曲线。

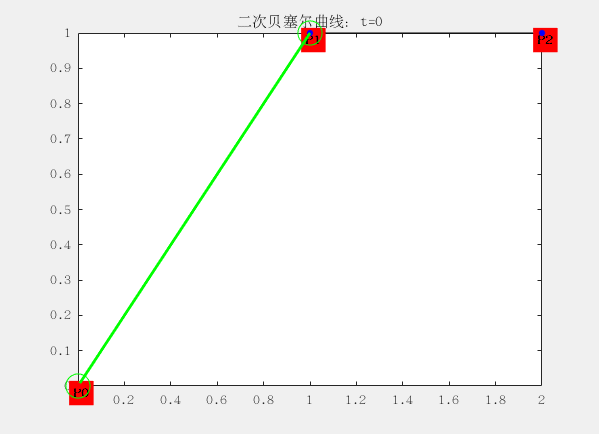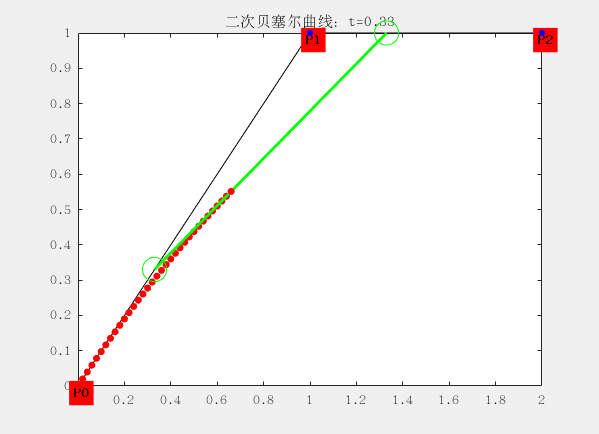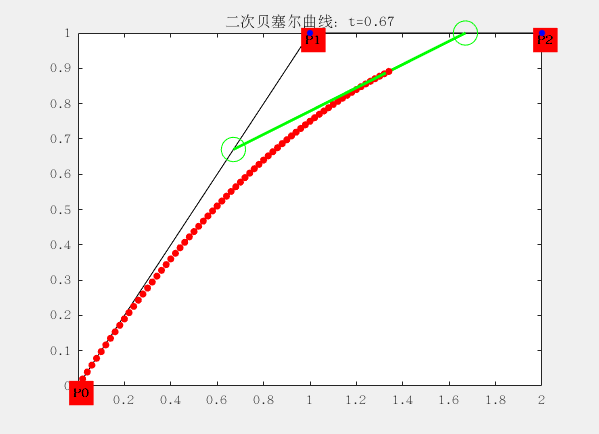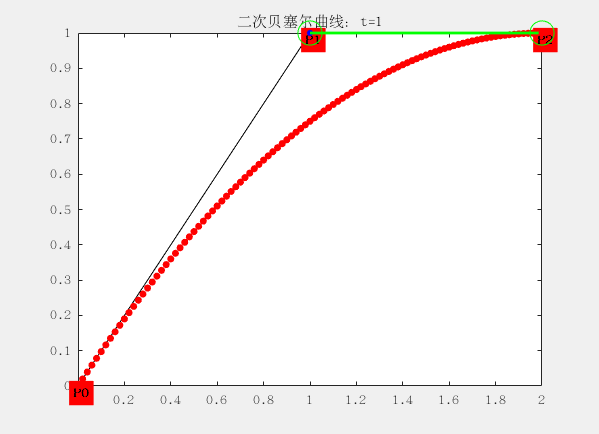
对应的曲线方程为：

$$ P_a = (1 - t) P_0 + tP_1 = P_0 + (P_1 - P_0)t $$

$$ P_b = (1 - t) P_1 + tP_2 = P_1 + (P_2 - P_1)t $$

$$ P_t = (1 - t) P_a + tP_b = P_a + (P_b - P_a)t $$

这是一条迭代公式，每次迭代都会少掉一个“点”。

最后得：

$$ B\big( t \big) = P_t = (1 - t)^2 P_0 + 2t(t -1)P_1 + t^2 P_2 $$

三阶：

有四个控制点

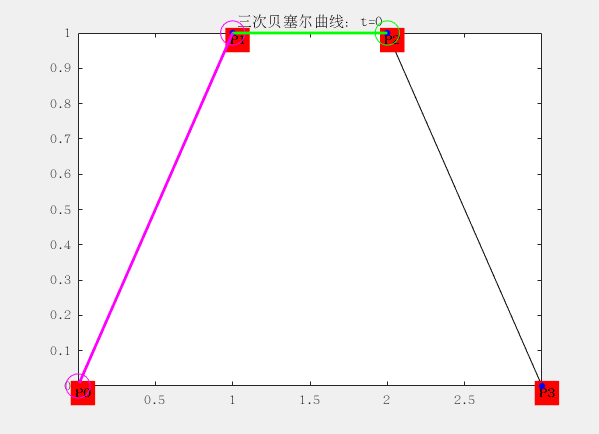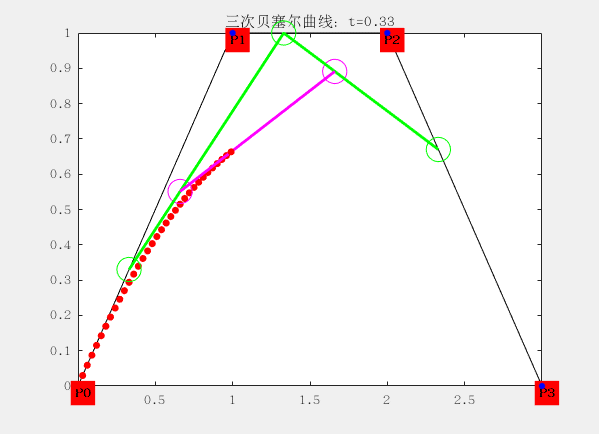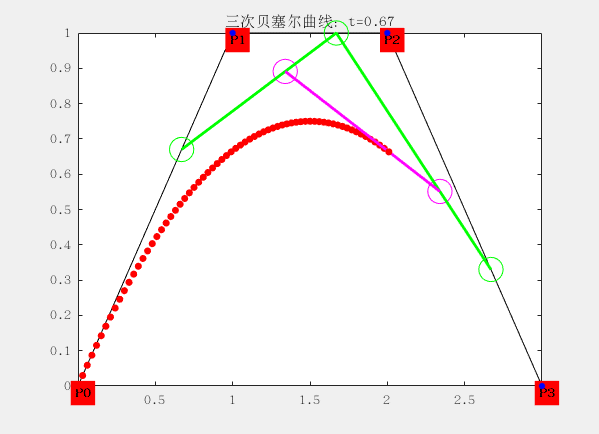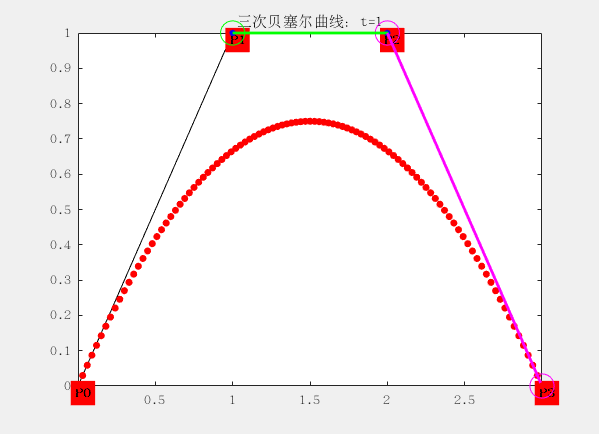
设控制点为P0，P1，P2和P4，曲线方程为：

$$ B\big( t \big) = P_t = (1 - t)^3 P_0 + 3t(t -1)^2t P_1 + 3t^2(1-t) P_2+t^3P_3 $$

配图这是matlab生成的gif动画，大家想要的也可以找我，代码私发给大家。

N阶：

我们发现，实际上是每轮都是 n 个点，形成 n-1 条线段，每个线段上有一个点在运动，那么就只关注这 n-1 个点，循环往复。最终只剩一个点时，它的轨迹便是结果。

如此一来，你会发现贝塞尔曲线内的递归结构。实际上，上述介绍的分别是一阶、二阶、三阶的贝塞尔曲线，贝塞尔曲线可以由阶数递归定义。

N阶贝塞尔曲线公式:

$$ B\big( t \big) = \sum\limits_{i=0}^{n} \big(_{i}^{n} \big) P_i(1-t)^{n-i} t^i ,t\in [0,1]$$

贝塞尔曲线应用

贝塞尔曲线在动画中有应用，前端以及一些其他显示要求；此外在路径规划过程中，也会使用贝塞尔曲线进行规划好路径再优化，我就是使用了后者进行优化规划好的路径，使得机器行走更加顺畅，不过使用中大家需要按照机器实际相应来进行调整t的精度以及阶数。

由于贝塞尔曲线本身的数学表达式便是一条递归式，所以决定采用递归的方式来实现。代码如下，BezierCurve函数实现贝塞尔曲线迭代，UseBezierOptimizePath函数的第二个参数进行控制使用的阶数，最后调用opencv实现可视化效果。

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core.hpp>
#include <vector>
using namespace cv;
using std::cout;
using std::endl;
using std::vector;

template <typename T>
T BezierCurve(T src)
{
    if (src.size() < 1)
        return src;
    const float step = 0.003;//1.0/step
    T res;
    if (src.size() == 1) {//递归结束条件
        for (float t = 0; t < 1; t += step)
            res.push_back(src[0]);
        return res;
    }
    T first_part{};
    T second_part{};
    first_part.assign(src.begin(), src.end() - 1);
    second_part.assign(src.begin() + 1, src.end());

    T pln1 = BezierCurve(first_part);
    T pln2 = BezierCurve(second_part);
    for (float t = 0; t < 1; t += step)
    {
        typename T::iterator::value_type temp{};
        temp += pln1[cvRound(1.0 / step * t)] * (1.0 - t) ;
        temp += pln2[cvRound(1.0 / step * t)] * t;
        res.emplace_back(temp);
    }
    return res;
}
template <typename T>
T UseBezierOptimizePath(T path,uint8_t order_number)
{
    if(path.size() < order_number)
        return {};
    T new_path{};
    for(uint8_t i=0;i<path.size()-(order_number-1);i+=(order_number-1))
    {
        T tmp = BezierCurve(T(&path[i],&path[ i + order_number]));
        new_path.insert(new_path.begin(),tmp.begin(),tmp.end());
    }

    return new_path;
}

int main(int argc, char const* argv[])
{
   while (1) {
        cout<< endl;
       cout<< endl;
       cout<< endl;
       vector<Point2f> path;
       RNG rng;

       for (int i = 1; i <8; i++)
           path.push_back(Point2f(i * 800 / 8, random() % 800));//rng.uniform(0,800)));//cvRandInt(rng) % 800));
       Mat img(900, 1200, CV_8UC3);
       img = 0;

       for(uint8_t i =0;i < path.size() -1;i++)
       {
            cout<< path[i]<< ","<< endl;
	        line(img,Point(path[i].x, path[i].y),Point(path[i+1].x, path[i+1].y), Scalar(255, 0, 0), 16, LINE_AA, 0);
       }
       cout<< endl;
    //    imshow("line", img);
       for (int i = 0; i < path.size(); i++)
           circle(img, path[i], 3, Scalar(0, 0, 255), 10); //BGR

    //    vector<Point2f> bezierPath = bezierCurve(path);
       vector<Point2f> bezierPath = UseBezierOptimizePath(path,4);
       for (int i = 0; i < bezierPath.size(); i++) {
        //    circle(img, bezierPath[i], 3, Scalar(0, 255, 255), 3); //BGR
           img.at<cv::Vec3b>(cvRound(bezierPath[i].y), cvRound(bezierPath[i].x)) = { 0, 255, 255 };
        //    printf("pose(%f %f)\n",bezierPath[i].x,bezierPath[i].y);
            imshow("black", img);
            // waitKey(10);
       }
       if (waitKey(0) == 'q')
           break;
   }
   return 0;
}

显示效果如下：

三阶

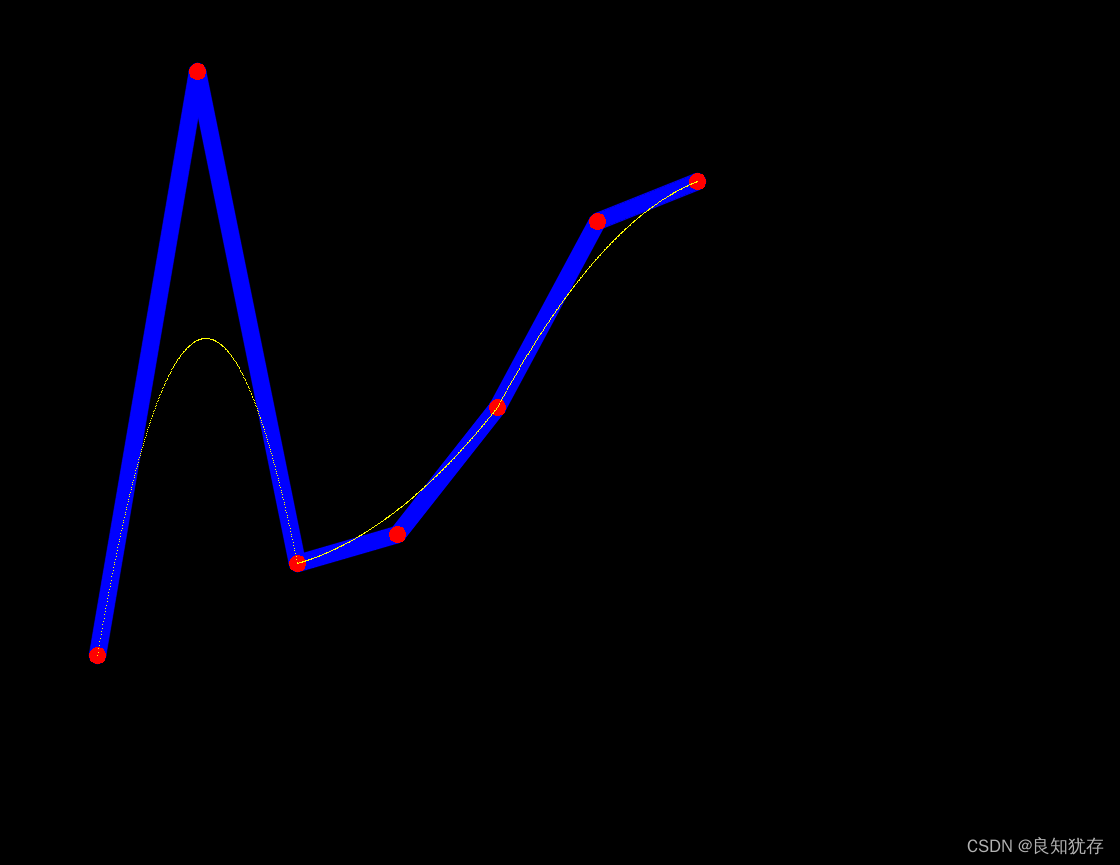
四阶

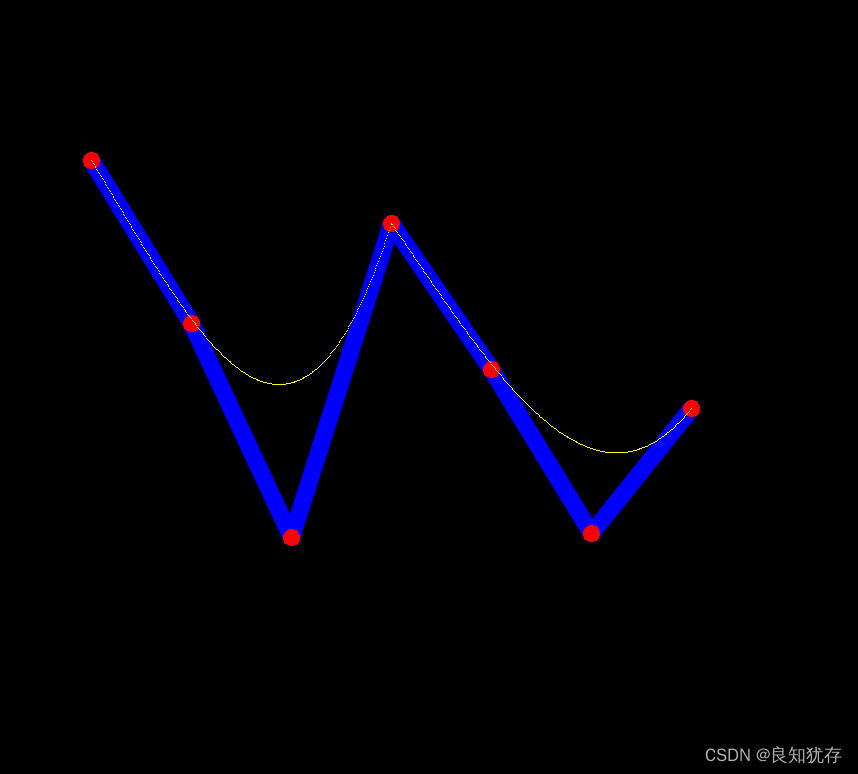
结语

这就是我自己的一些设不贝塞尔曲线的使用分享。如果大家有更好的想法和需求，也欢迎大家加我好友交流分享哈。

---

作者：良知犹存，白天努力工作，晚上原创公号号主。公众号内容除了技术还有些人生感悟，一个认真输出内容的职场老司机，也是一个技术之外丰富生活的人，摄影、音乐 and 篮球。关注我，与我一起同行。

                              ‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧  END  ‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧‧

推荐阅读

【1】jetson nano开发使用的基础详细分享

【2】Linux开发coredump文件分析实战分享

【3】CPU中的程序是怎么运行起来的 必读

【4】cartographer环境建立以及建图测试

【5】设计模式之简单工厂模式、工厂模式、抽象工厂模式的对比

本公众号全部原创干货已整理成一个目录，回复[ 资源 ]即可获得。