J - Intersection

来源poj 1410

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example:

line: start point: (4,9)

end point: (11,2)

rectangle: left-top: (1,5)

right-bottom: (7,1)

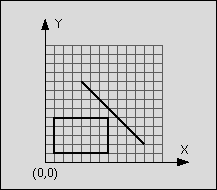
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format:

xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1

4 9 11 2 1 5 7 1

Sample Output

F

很坑，如果相交或者在矩形里面就是T，否者就是F；

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include <iomanip>
#include<cmath>
#include<float.h>
#include<string.h>
#include<algorithm>
#define sf scanf
#define pf printf
#define mm(x,b) memset((x),(b),sizeof(x))
#include<vector>
#include<queue>
#include<stack>
#include<map>
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=a;i>=n;i--)
typedef long long ll;
const ll mod=1e9+100;
const double eps=1e-8;
using namespace std;
const double pi=acos(-1.0);
const int inf=0xfffffff;
struct point
{
	int x,y;
};
int direction(point p1,point p2,point p3)//p1是向量起点，p2是终点，p3是判断点，>0则在左边＜0在右侧
{
return (p1.x-p3.x)*(p2.y-p3.y)-(p1.y-p3.y)*(p2.x-p3.x);
}
int main()
{
	int n;
	cin>>n;
	while(n--)
	{
		point a[4],t1,t2;
		int x1,x2,y1,y2;
		sf("%d%d%d%d",&t1.x,&t1.y,&t2.x,&t2.y);
		sf("%d%d%d%d",&x1,&y1,&x2,&y2);
		if(x1>x2)
		swap(x1,x2);
		if(y1<y2)
		swap(y1,y2);
		a[0].x=x1;a[0].y=y1;
		a[1].x=x1;a[1].y=y2;
		a[2].x=x2;a[2].y=y2;
		a[3].x=x2;a[3].y=y1;
		if(t1.x>x1&&t2.x>x1&&t1.y<y1&&t2.y<y1&&t1.x<x2&&t2.x<x2&&t1.y>y2&&t2.y>y2)
		pf("T\n");
		else if((t1.x<x1&&t2.x<x1)||(t1.x>x2&&t2.x>x2)||(t1.y>y1&&t2.y>y1)||(t1.y<y2&&t2.y<y2))
		pf("F\n");
		else if((direction(t1,t2,a[0])>0&&direction(t1,t2,a[1])>0&&direction(t1,t2,a[2])>0&&direction(t1,t2,a[3])>0)||(direction(t1,t2,a[0])<0&&direction(t1,t2,a[1])<0&&direction(t1,t2,a[2])<0&&direction(t1,t2,a[3])<0))
		pf("F\n");
		else
		pf("T\n");
	}
	return 0;
}